Тепловой потенциал  с плотностью
с плотностью  называется поверхностным тепловым потенциалом (простого слоя с плотностью
называется поверхностным тепловым потенциалом (простого слоя с плотностью  ),
),

Если  - ограниченная функция в
- ограниченная функция в  , то поверхностный тепловой потенциал
, то поверхностный тепловой потенциал  существует в
существует в  , принадлежит классу
, принадлежит классу  , представляется интегралом Пуассона:
, представляется интегралом Пуассона:
 (2.30)
(2.30)
Постановка задачи Коши для уравнения теплопроводности.
 (2.31)
(2.31)
 (2.32)
(2.32)
Считаем 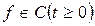 и
и  . Предположим, что существует классическое решение
. Предположим, что существует классическое решение  этой задачи. Это значит, что
этой задачи. Это значит, что  , удовлетворяет уравнение (2.31) при
, удовлетворяет уравнение (2.31) при  и начальное условие (2.32) при
и начальное условие (2.32) при  .
.
Продолжая функции  и
и  нулём при
нулём при  , заключаем, что продолженные функции
, заключаем, что продолженные функции  и
и  удовлетворяют в
удовлетворяют в  уравнению теплопроводности:
уравнению теплопроводности:
 (2.33)
(2.33)
Равенство (2.33) показывает, что начальное возмущение  для функции
для функции  играет роль мгновенно действующего источника
играет роль мгновенно действующего источника  (типа простого слоя на плоскости
(типа простого слоя на плоскости  ) и классические решения задачи Коши (2.31) - (2.32) содержатся среди тех решений уравнения (2.33), которые обращаются в нуль при
) и классические решения задачи Коши (2.31) - (2.32) содержатся среди тех решений уравнения (2.33), которые обращаются в нуль при  . Это даёт основание ввести следующее обобщение задачи Коши для уравнения теплопроводности.
. Это даёт основание ввести следующее обобщение задачи Коши для уравнения теплопроводности.
Обобщённой задачей Коши для уравнения теплопроводности с источником  назовём задачу о нахождении обобщённой функции
назовём задачу о нахождении обобщённой функции  , обращающейся в нуль при
, обращающейся в нуль при  и удовлетворяющей уравнению теплопроводности
и удовлетворяющей уравнению теплопроводности
 (2.34)
(2.34)
Уравнение (2.34) эквивалентно следующему:
Для любой  справедливо равенство:
справедливо равенство:
 (2.35)
(2.35)
Из уравнения (2.34) следует, что необходимым условием разрешимости обобщенной задачи Коши является обращение в нуль  при
при  .
.
Решение задачи Коши.
Пусть  , где
, где 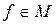 и
и  - ограниченная функция в
- ограниченная функция в  . Тогда решение соответствующей обобщённой задачи Коши существует и единственно в классе
. Тогда решение соответствующей обобщённой задачи Коши существует и единственно в классе  и представляется формулой Пуассона:
и представляется формулой Пуассона:
 (2.36)
(2.36)
Таким образом, общее решение распределения интересующего нас потока по координате и времени в аналитическом диффузионном приближении может быть представлено в виде двух функций, одна из которых характеризует форму потока в начале координат, вторая характеризует изменения потока во времени, f(x, t)и θ(t) определяются из общей постановки задачи и индивидуальны для каждого потока.
Во многих случаях, решение можно представить в виде сумы конечного ряда:
 , (2.37)
, (2.37)
где Ф(x, t) – интеграл ошибок.
В более сложных случаях решение может быть выражено в виде бесконечных рядов, полиномов Лежандра, функции Бесселя, Ханкеля или других специализированных функций. Однако такое представление выходит за рамки нашего курса.
Численное решение уравнений переноса в диффузионном приближении.
В тех случаях, когда среду нельзя представить в виде уравнений с постоянными коэффициентами, или граничные условия нельзя представить в виде среды с бесконечно распространяющимися потоками, используют более сложную форму.
 , (2.38)
, (2.38)
где  - удельная емкость исследуемого потока (теплоёмкость),
- удельная емкость исследуемого потока (теплоёмкость),
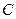 - удельная проводимость исследуемого потока (теплопроводность),
- удельная проводимость исследуемого потока (теплопроводность),
 - источник потока,
- источник потока,
 - коэффициент связывающей скорость прохождения потока в веществах, имеющих различные свойства (коэффициент теплопроводности),
- коэффициент связывающей скорость прохождения потока в веществах, имеющих различные свойства (коэффициент теплопроводности),
 - скорость переноса потока.
- скорость переноса потока.
Во многих случаях, применим набор граничных условий, который позволяет, не выясняя, что происходит на удаленных границах, ставить задачу, которая описывает процесс с качеством, достаточным для наших целей. Такая постановка особенно важна в случае моделирования процессов проходящих при высоких температурах, давлении или в средах, имеющих высокую степень агрессивности, где затруднено непосредственное измерение параметров.
В этих случаях можно предположить, что:
1. Потоки на невзаимодействующих границах просто отражаются от стенки. Такое приближение называется «зеркально отражающая граница». В этом случае предполагается, что мы можем поставить следующие граничные условия:

 , (2.39)
, (2.39)
где Uгр+- - соответствует интенсивности прямого и отраженного потока на удаленной границе;
tгр – время за которое поток достигает границы.
2. Все потоки на удаленной границе равны нулю – абсолютное поглощение.
 = 0 (2.40)
= 0 (2.40)
В этом случае уравнение решается численно с помощью достаточно простых сеточных методов. Однако граничные условия на взаимодействующей границе лучше выбирать, используя решение в аналитическом приближении в узкой области у границы раздела. Определение величины этой области выбирается следующим методом.
Определяется, для каких x и t нашей задачи справедливо выражение:
(2.41)
В этом случае аналитическое решение изменяется вместе с изменением входных параметров и применимо как граничное условие для более точного решения.






