Понятие объекта, системы, процесса не имеет однозначно точного определения. В жизни мы постоянно занимаемся моделированием, заменяя реальные процессы их различными аналогами, например, кредитная карточка является аналогом денежных знаков, а перед постройкой любого сложного объекта создают его макет. Однако в данном курсе мы дадим определение, которое позволит нам описать и построить математическую модель, чаще всего используемую для расчетов, исследований и изучения объектов с помощью математики в областях, связанных с авиаприборостроением.
Определение 1. Системой (объектом, процессом) называется все, что подчиняется определённым законам и может быть описано математическим аппаратом.
Очевидно, если система подчиняется какому-либо известному нам закону, то существует некий математический аппарат, который позволяет описать эту систему. Исходя из этого, мы можем дать определение модели системы.
Определение 2. Система (объект процесс) описанный в терминах математики называется математической моделью.
В данном курсе будут рассмотрены типовые модели, которые чаще всего используются в технологии авиаприборостроения.
Классификация моделей.
Можно выделить 3 типа моделей, чаще всего встречающихся при решении практических задач.
К первому типу моделей относятся модели представляющие набор уравнений, эмитирующих физические процессы, математическое описание которых выведено на основе общих законов сохранения неравновесной термодинамики.
Ко второму типу моделей относятся имитационные пошаговые модели. Чаще всего основой такого моделирования составляет математический аппарат операционного вычисления, к которому относится, в частном случае, линейное и динамическое моделирование.
Третий тип моделей представляет собой аналоговое моделирование, при котором часть данных вводимых в модель получена экспериментально, а другая часть данных - представляет собой функцию, разложенную в ряд. Различают два способа построения такой модели:
1. Анализ, сделанный с помощью математической статистики, частным случаем этого способа является обычный регрессионный анализ.
2. Аналоговое моделирование, когда физические процессы заменяются узлами - аналогами электронной схемы и вычисление проводится с помощью расчета системы дифференциальных уравнений.
Модели реальных процессов не могут быть построены с использованием только какого-то одного метода. Основными причинами этого является:
- сложность физических процессов, происходящих при работе приборов;
- отклонения экспериментальных данных от данных, записанных уравнениями детерминированных законов, которые связано с наличием различных статистических погрешностей;
- сложность уравнений моделей, которые часто невозможно решить из-за слишком большого числа переменных и сложности функций, описывающих моделируемый процесс;
- во многих технологических процессах вводимые параметры часто определить невозможно из-за условий прохождения процесса (высокая температура, плазменное состояние, вредность процесса).
Таким образом, полное математическое моделирование системы (объекта, процесса) представляет собой некорректно проставленную задачу. Однако, для решения конкретных задач необходима только часть результатов этой модели, которую можно получить, используя упрощенное представление системы (объекта, процесса). Это представление называется приближением.
Выбор приближения является одной из самых серьезных задач математического моделирования. Ошибка в выборе приближения выясняется только на конечном этапе и делает работу непригодной для использования.
Выбор приближения модели.
Выбор приближения (ВП) условно можно разделить на две части:
- выбор физического приближения, в котором упрощаются законы, описывающие систему (объект, процесс);
- выбор математического приближения, в котором упрощается математический аппарат, описывающий систему (объект, процесс).
ВП начинается с изучения объекта, процесса или системы, для которой производится модель. Исследуемые системы (объекты, процессы) условно можно разделить на три типа:
1. Находящиеся в процессе проектирования и создания. В этом случае нас интересуют любые сведения о физике процесса, возможных реализациях конструкции, возможных точностных параметрах. При этом мы стараемся описать наибольшее количество известных нам процессов, что приводит к чрезвычайной сложности уравнений. Несмотря на такое точное описание, полученная модель имеет только качественный характер из-за неопределенности вводимых параметров и начальных данных. Поэтому не имеет смысла получать точное решение уравнений, упрощение можно провести за счет упрощения математического аппарата.
2. Реализованные системы (объекты, процессы) подвергающиеся модернизации. В этом случае описание уже изученных процессов можно провести аналоговым методом. Исходные данные можно экспериментально уточнить. Однако, в этом случае, требуется количественная информация, которую приходится получать за счет более точного решения математических уравнений, очень часто это решение осуществляется количественным способом.
3. Широко используемые системы (объекты, процессы), для которых чаще всего требуется оптимизация или определение погрешностей. В этом случае для моделирования используется аппарат математической статистики.
Изучение и моделирование системы (объекта, процесса) осуществляется поэтапно:
На первом этапе изучаются исходные данные, и определяется конкретная цель моделирования, выбирается основной тип моделирования, с которым мы будем работать дальше.
На втором этапе мы пытаемся связать параметры модели с выходными характеристиками системы (объекта, процесса), которые определяются на основе статистической обработки известных экспериментальных данных. При этом иногда приходится дополнительно строить статистическую модель объекта.
На третьем этапе записывается математическая модель в наиболее общем виде, и анализируются физические процессы с точки зрения степени влияния на систему. На этом этапе моделирования большую помощь может оказать построение промежуточных имитационных моделей. На основе этого этапа можно сделать декомпозицию процесса, которая ляжет в основу последующего упрощения уравнений модели.
В дальнейшем при практическом моделирования на каждом этапе выбирается один тип математического аппарата моделирования, но на различных этапах можно переходить от одного типа моделирования к другому. При этом результаты предыдущего этапа моделирования служат входными данными для последующего.
Выбор математического приближения.
После постановки общей задачи мы получаем систему уравнений, которую, в большинстве случаев, не можем решить, т.к. количество уравнений слишком велико, а время на их решение ограничено. Поэтому мы вынуждены упрощать эти уравнения. Правильно проведенное упрощение не приводит к понижению точности модели, поскольку эта точность, в первую очередь, существенно ограничивается точностью исходных данных и входным набором параметров.
В каждом конкретном случае выбор математического приближения является достаточно сложной и оригинальной задачей. Можно привести только общие рекомендации по его реализации:
1. Перейти от тензорных и векторных уравнений к скалярным, т.е. понизить порядок размерности задачи.
2. При наличии известного статистического распределения, например, распределения частиц по энергии и т. д., часть уравнений системы можно заменить этими распределениями.
3. Если позволяют условия задачи, можно подобрать граничные условия, которые сделают задачу эквивалентной стандартным приближениям, математическое решение которых, как правило, дано в литературных источниках. Стандартные приближения будут даны ниже. Основная ошибка происходит из-за того, что в типовых стандартных приближениях не указываются те физические эффекты, которыми мы пренебрегаем. Если в нашей задаче этот эффект играет большую роль, данное приближение может дать результат далекий от практики. Причем подобные ошибки становятся заметными только на последних этапах моделирования, часто уже на этапе модельной реализации макетного образца, что приводит к серьезным потерям времени и финансов.
Если модель описывается в рамках детерминированных законов, одним из типов упрощения математической модели может быть упрощение уравнений за счет пренебрежения слабодействующими эффектами. Однако для проведения этих упрощений необходимо провести предварительные оценки. Методика проведения данных оценок [1].
Как правило, количество уравнений после проведения этого этапа уменьшается в 3 - 4 раза, однако система все равно остаётся сложной.
Следующие упрощения не являются обязательными и их применение связано с нехваткой временина разработку модели и степенью владения математическим аппаратом разработчиком.
Они могут понизить адекватность модели, поэтому перед их применением необходимо провести анализ основных целей моделирования. Если поставленная цель может быть достигнута на уровне качественной модели, то применение нижеописанных преобразований оправдано. Эти преобразования сильно сокращают время на решение задачи, поскольку общие алгоритмы решения и стандартные модели можно найти в приложениях к таким известным пакетам как MathCad, MathLab.
Данное преобразование заключается в разделении физических процессов. Например, при если происходит диффузионное перемещение массы из одной среды в другую при повышении температуры, мы полагаем, что диффузионный процесс и тепловые процессы разделены по времени. Математически это выражается тем, что функция U(x,y), зависящая от двух переменных (U - результат моделирования, x - диффузионный процесс, y - тепловой процесс), превращается в две функции U(x) и U(y). Как правило, это возможно сделать в основной массе задач, где перекрёстными членами по вторым производным можно пренебречь. Более подробно методика данных преобразований дана в работе [1].
В том случае общая система уравнений, превращаются в две отдельные системы уравнений, каждая из которых зависит только от независимой переменной x или y. Следовательно, их можно преобразовать в дифференциальные уравнения полных производных. Методы решения дифференциальных уравнений полных производных хорошо разработаны и даны в виде приложений к стандартным пакетам (MathCad, MathLab).
Следующее необязательное для использования приближения связано с постановкой граничных условий.
Как правило, как будет далее показано, при постановке граничных условий часто возникает «скачок» на границе области интегрирования. Это приводит к трудностям в численном решении уравнений, связанным с особенностями компьютерного моделирования. Поэтому граничные условия для данной системы ставятся так, что бы можно было получить аналитическое решение в явном виде. Это аналитическое решение используют как граничное условие для более общей задачи.
Во многих случаях подобное решение дает ответ на многие вопросы, касающиеся разработки системы, хотя количественные результаты расчетов не совпадают с экспериментальными данными. Проведение такого анализа может совместить по времени решение более сложной задачи по моделированию данной системы (объекта, процесса) и начальные разработки по ее практической реализации.
Введенные упрощения позволяют представить задачу в виде системы уравнений:
,
где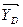 
- система написана на основе детерминированных законов;
- система уравнений, основанная на случайной составляющей.
Подход к моделированию этих составляющих различен, поэтому, если
>> ,
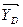то ограничиваются моделированием только детерминированной части процесса. Если YD – хорошо изученная функция и нас интересуют только ошибки, то ограничиваются моделированием только случайной части процесса. Решение более сложных задач выходит за рамки нашего курса. Однако математические подходы к этим задачам даны в работе [1].
Моделирование детерминированной части задач.
Существует два типа математического аппарата, на основе которого производится моделирование детерминированной части задач.
Первый тип основан на законах статистической физики. Основная идея этого подхода заключается в том, что физические законы выводятся для большого ансамбля частиц. При этом взаимодействиями между частицами внутри системы пренебрегают. В результате моделирования получается статистическое распределение параметров системы по различным функциям от времени и координат. Подобным моделированием занимаются в основном при разработке фундаментальных законов, и оно выходит за рамки нашего курса. Однако в некоторых случаях мы будем использовать некоторые статистические распределения, полученные ранее на основе выведенных законов.
Второй тип моделирования заключается в описании системы на основе различных фундаментальных законов сохранения (массы, энергии, скорости). В этом случае, система уравнений представляет собой сложное интегро-дифференциальное тензорное уравнение, которое принципиально не решается в общем виде. На практике разработано значительное количество способов формального упрощения таких систем, которые называются типовыми приближениями. При этом часть приближений носит фундаментальный характер и, как правило, допустимость его предполагается априори заданной, а часть приближений носит индивидуальный характер, связана с решаемой задачей, и применимость этих решений обязательно должна быть оценена разработчиком. С некоторыми типами наиболее часто применяемых при моделировании приближений мы ознакомимся в нашем курсе.
Понятие об обобщенных переменных.
Реально, математическая постановка задачи не связана с ой конкретной областью, в которой производится моделирование. Оптические задачи и движение жидкости могут описываться одинаковыми уравнениями. Этими вопросами занимается теория подобия [2].
В данном курсе мы введем понятие только об обобщенных переменных, которые позволяют описывать одинаковыми уравнениями любой процесс в рамках детерминированного приближения [3].
Определение 5 Обобщенныминазываются переменные, значение которых не зависит от реального объекта, а связано только с представлением о физическом взаимодействии.
Определение 6 Обобщенной силой называется фактор, воздействующий на данный объект.
Определение 7 Обобщенной скоростью (ускорением) называется функция, характеризующая изменение положение данного фактора в заданном координатном пространстве.
Определение 8 Обобщенной координатным пространством называется координатная система, в которой происходит изменение параметров исследуемого фактора (количество обобщенных координат не ограничено).
Моделирование детерминированных задач использует обобщенные переменные как независимые факторы, для которых известны физические законы. Для многих задач физические законы описываются в приближении неравновесной термодинамики. Эти приближения отличаются от приближения равновесной термодинамики следующими положениями:
1. В среде существует бесконечно малый объем, в котором выполняется «локальный закон равновесия фаз», т.е. применимо приближение равновесной термодинамики. Параметры среды представляют собой непрерывную функцию вместе со своими производными. Общая среда не является равновесной системой.
2. В данном локальном объеме работают те же законы, что и в равновесной термодинамике (законы сохранения энергии, массы, энтропии). На базе этих законов, записанных в дифференциальной форме, выводятся основные уравнения для моделей, которые описывают уже не локальные объемы, а непрерывную среду конечного размера.
Рассмотрим основные законы сохранения в приближении неравновесной термодинамики.
