Стационарные состояния, т. е. такие состояния, в которых параметры, их определяющие, не зависят от времени, играют важную роль в практических приложениях. Стационарные состояния могут быть как равновесными, так и неравновесными в зависимости от граничных условий, накладываемых на систему.
До рассмотрения стационарных состояний мы обсудим некоторые свойства состояния механического равновесия.
В [3] показано, что стационарные неравновесные состояния являются устойчивыми по отношению к возмущениям. Это обстоятельство представляет собой обобщение принципа Ле Шателье—Брауна для равновесных состояний.
Механическое равновесие
Для случая состояния механического равновесия можно доказать теорему, упрощающую описание некоторых необратимых процессов, в частности явлений диффузии.
Состояние механического равновесия есть состояние, в котором ускорение dv/dt равно нулю. Мы интересуемся такими состояниями механического равновесия, в которых не только ускорения равны нулю, но и пренебрежимо малы градиенты скоростей, а, следовательно, мал и вязкий тензор давлений П.
Для таких состояний уравнение движения (2.19) принимает вид:
0=:-grad p + 
(2.1)
В ряде важных случаев состояние механического равновесия, описываемое уравнением (2.1), действительно устанавливается за время, значительно меньшее времени, характерного для термодинамических процессов. Таким образом, фактически это состояние достигается уже к началу исследуемых необратимых процессов. Для более общих случаев это утверждение не всегда справедливо: все зависит от конкретной физической ситуации. Можно представить себе, например, осциллирующие системы, в которых ускорение все время отлично, от нуля. Однако, например, для явлений диффузии или термодиффузии в замкнутых сосудах вполне разумно предполагать, что в хорошем приближении состояние механического равновесия, описываемое уравнением (2.1), быстро реализуется. В диффузионных экспериментах ускорение dv/dt может быть отличным от нуля, например, в том случае, когда молекулярные массы участвующих в процессе компонентов имеют разную величину. Однако это ускорение очень мало и возникающие градиенты давления (если предположить отсутствие внешних сил) также пренебрежимо малы. Налагаемая в начальный момент разность давлений также приведет к появлению ускорений, но они исчезнут вследствие наличия вязкости задолго до того, как процесс диффузии достигнет стационарного состояния. Таким образом, вновь предполагая отсутствие внешних сил Fk, мы можем считать градиенты давления пренебрежимо малыми уже почти в самом начале процесса диффузии.
Для состояния механического равновесия (2.1) Пригожин [4] доказал теорему, согласно которой в выражении для производства энтропии (4.13) массовую скорость v. входящую в определение (2.9) диффузионного потока Jk, можно заменить другой произвольной скоростью vа.
Доказательство этой теоремы основано на справедливости следующего равенства:
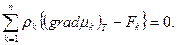(2.2)
Это равенство легко получается, если заметить, что для удельной функции Гиббса:
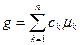(2.3)
имеем:
(2.4)
Из (2.3) и (2.4) следует соотношение Гиббса—Дюгема:
(2.5)
или
(2.6)
Стационарные состояния
Подставляя grad p из уравнения движения (2.1) для случая механического равновесия в последнее соотношение, получаем (2.2).
Теорема Пригожина получается отсюда совсем просто. Действительно, диффузионный Член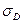 
, представляющий собой источник энтропии неравновесной системы [4], с подстановкой выражения (2.9) для Jk имеет вид:
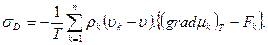
(2.7)
Это соотношение эквивалентно следующему:
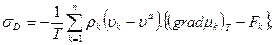(2.8)
где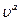 
— произвольная скорость, так как разность между (2.7) и (2.8), согласно (2.2), равна нулю. Равенство соотношений (2.7) и (2.8) доказывает теорему Пригожина. Эта теорема нам понадобится при обсуждении многочисленных явлений, связанных с процессами диффузии. Заметим, наконец, что внешнюю силу Fk мы считали консервативной силой.
Таким образом, мы можем поставить граничные условия в общей задаче исходя из того, что существует поверхность, где осуществляется состояние равновесия. Для твердых тел (балки) - это состояние механического равновесия, где поверхность твердого тела неподвижна. Для систем представляющих собой фазовый переход – это состояние термодинамического равновесия, чаще всего оно реализуется на границе раздела фаз. Это можно пояснить, используя основное положение неравновесной термодинамики, которое гласит, что существует бесконечно малый объем, в котором система находится в равновесии. Используя это положение, статистическая физика показывает, что если в системе нет резких сильных источников энергии, то в близи раздела фазы существует граница, где обе фазы находятся в равновесии, даже если в общем объеме фазы находятся в состоянии далеком от равновесного. Чем дальше фазы от состояния равновесия, тем тоньше эта граница. Это положение в литературе известно как «закон локального сохранения фаз». Опытным путем было показано, что отклонение от этого закона реализуется только в технологических системах получения материала в космосе и ядерных реакциях, а также при применении мощных лазеров пико- и наносекундных импульсов. Во всех остальных случаях закон локального равновесия фаз не нарушается, и мы можем им пользоваться без объяснений и доказательств. Наиболее интересны возможности по применению этого закона для моделирования роста лазерных кристаллов и технологий обработки лазером различных поверхностей. Он позволяет во многих случаях ограничиться моделированием системы (объекта, процесса) только в равновесном приближении.
