Після побудови гістограми і статистичної кривої густини по її зовнішньому вигляду можна припустити, що закон розподілу ймовірностей відповідає тому чи іншому відомому закону. Але це припущення потребує перевірки, яка базується на наступному основному положенні. Якщо при статистичному спостереженні були відмінності в розподілі ймовірностей у порівнянні з теоретичною кривою для припустимого закону, то ці відмінності можуть бути викликані двома причинами:
1)число випробувань невелике, тобто статистичні кількісні характеристики і закон розподілу відрізняються від теоретичних значень в тій мірі, в якій це закономірно при заданому числі випробувань;
2)невірне саме припущення про закон розподілу ймовірностей.
Щоб визначити, яка з причин викликає вказані відмінності, застосовують критерії згоди. Для кожного критерію вибирають певну величину міри розбіжності, яка виражає ступінь розбіжності між спостережуваним законом і відомим законом розподілу, який використовується як імовірний. Далі для теоретичного закону розподілу знаходять при різних числах випробувань n імовірностей того, що міра розбіжності дорівнює чи більша деякого числа, і складають таблиці ймовірностей міри розбіжності при даному числі випробувань n-V. Визначають міру розбіжності фактично спостережену для отриманого статистичного матеріалу v. З отриманої таблиці ймовірностей V знаходять імовірність, що відповідає значенню v (v=V). Якщо вона достатньо велика, наприклад, 0,8÷0,9 і більше, то відмінність від теоретичного закону отримана лише за рахунок малої кількості випробувань і гіпотеза, що була прийнята раніше, правдоподібна; якщо ж імовірність v=V мала (0,2÷0,1 і менша), то це означає, що відмінності від теоретичного закону викликані не обмеженим числом випробувань, а невірним припущенням, тобто гіпотеза прийнята невірно.
Критерії згоди
Розглянемо критерій Колмогорова. За цим критерієм визначають величину D, яка дорівнює максимальному значенню абсолютної величини різниці між статистичною і теоретичною функціями розподілу.
Потім визначають міру розбіжності:
,
де n – число випробувань;
і звертаються до таблиць імовірності того, що для теоретичної функції розподілу при заданій кількості випробувань мірі розбіжності буде рівна чи менша λ.
Доведено, що така ймовірність не залежить від характеру теоретичної кривої розподілу. Тому для будь-якої гіпотези можна використовувати критерій Колмогорова.
Критерій Пірсона (
) дає можливість оцінити розбіжність між статистичним розподілом і теоретичним:
= 
або = 
; 
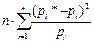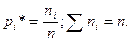
Якщо р дуже мале, то розбіжність за рахунок випадкових причин залежить від параметра r, який називається числом ступенів свободи; він береться рівним числу розрядів R мінус число незалежних умов (зв’язків), які накладені на частоти 
.
Критерій Смирнова - Колмогорова застосовують при оцінці однорідності вибору даних. Задача зводиться до перевірки належності N1 і N2 до однієї сукупності.
Будують F*(x) для кожної сукупності (групи даних).
Тоді визначають розбіжність:
і p(DNN > dNN).
Довірчий інтервал, довірча ймовірність.
На практиці часто потрібно дати не тільки точкову оцінку випадкової величини χ, тобто вказати точку на числовій осі, у якій повинно знаходитись значення невідомого параметра а, але й оцінити його точність і надійність.
Для визначення точності оцінки користуються довірчими інтервалами, а для визначення її надійності – довірчими ймовірностями.
; 
.
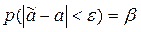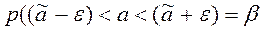Тобто, параметр а з імовірністю β потрапляє в інтервал:
,
де а – невипадкова, 
- випадкова величина, ширина - також випадкова величина.
Імовірність β є ймовірність того, що випадковий інтервал покриє точку а.
- довірчий інтервал; β - довірча ймовірність.
Отже, довірчою ймовірністюβ, яка відповідає даному довірчому інтервалу, називається ймовірність того, що дійсне значення параметра лежить у цьому інтервалі.
Побудуємо довірчий інтервал, що покриває невідомий параметр з заданою ймовірністю β.
В результаті досліду було отримано реалізації випадкових величин 
.
Їх середнє значення:
. 
Середнє квадратичне відхилення:
.
Враховуючи, що закон розподілу випадкової величини 
близький до нормального, то можна записати:
М(х)=а;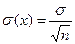 
.
Виходячи з цього, можемо записати довірчий інтервал:
; 
,
.
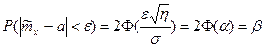α знайдемо з умови Φ(α)=β/2.
Тобто довірчий інтервал:
(β = 0,95;0,9;0,999).
