Досить часто випадкові величини є залежними, причому визначення однієї величини більш можливе, ніж іншої, що залежить від неї.
Якщо одна з випадкових величин набуває конкретного значення, то це не означає, що і друга набуває конкретного значення. Друга величина теж є випадковою величиною, але її імовірнісні характеристики набувають тих чи інших значень в залежності від конкретного значення першої випадкової величини.
Такими випадковими величинами в енергетиці є, наприклад, добовий виробіток енергії і добовий максимум навантаження енергосистеми, сумарне навантаження і температура зовнішнього повітря.
Таким чином, якщо дві випадкові величини ε і η набувають деяких значень x і y і є незалежними, то закон розподілу ймовірностей однієї з них не залежить від закону розподілу іншої. Якщо ж ці величини є залежні, то будь якому значенню однієї з них відповідає той або інший закон розподілу другої величини.
Залежність закону розподілу імовірностей однієї величини від значень іншої називається кореляційною залежністю.
Для системи випадкових величин, так як і для випадкових величин, вводяться поняття функції і густини розподілу.
Для двомірного вектора з координатами (ε; η):
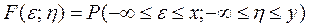
Графічно – імовірність попадання двомірного вектора на площині в квадрат з вершиною в точці (x; y), розміщеного лівіше і нижче точки.
Аналогічно, імовірність попадання в довільний пря-
мокутник, який обмежений точками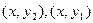 
:
Імовірність попадання двомірного вектора в деякий квадрат:
 | |||
 | |||
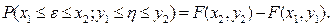
Функція розподілу системи випадкових величин є неспадна, причому:
F(-∞;-∞)=F(-∞;y)=F(x;-∞)=0,
F(+∞;+∞)=1,
F(+∞;y)=F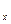 
(y),
F(-x;+∞)=F 
(x) – функція розподілу - компонент.
Густина розподілу:
.
Густина розподілу є невід’ємна функція і володіє такою властивістю:
.
На практиці часто розв’язують задачі, в яких визначають закон розподілу системи випадкових величин на основі законів розподілу її компонент. Причому закон розподілу компонент задається умовним законом розподілу.
Умовним законом розподілу будь-якої компоненти двомірного вектора називають закон розподілу, визначений за умови, що всі компоненти, крім вказаної, набули певного значення.
Числові характеристики
Розглянемо поняття моменту.
Початковий момент для дискретних і неперервних випадкових величин:
,
.
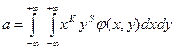Якщо k=s=1, то отримаємо вираз для математичного сподівання; геометрично – це є координати точки, відносно якої відбувається розсіювання двомірного вектора.
Центральний момент:
,
.
Якщо ks=2, то отримаємо дисперсію, якщо ks=1, то отримаємо центральний момент 1-го порядку, який називається кореляційним моментом або коваріацією (cov). Він характеризує зв’язок між випадковими величинами ε та η, а також їх розсіювання k (ε; η). Для незалежних величин k (ε; η) = 0.
Якщо одна з величин дуже мало відхиляється від свого математичного сподівання, то кореляційний момент буде малим, якою б тісною не була кореляційна залежність. Тому для характеристики зв’язку між випадковими величинами ε і η у чистому вигляді користуються так званим коефіцієнтом кореляції:
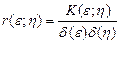- це є діагональна матриця, де δ(ε), δ(η) –стандартні відхилення компоненти, а r (ε;η) характеризує лише лінійну ймовірну залежність, тобто ступінь тісноти лінійної залежність між випадковими величинами (кореляційну).
Властивості:
1) для незалежних і залежних некорельованих випадкових величин
;
2) геометрично – середньодисперсійний компонент:
;
3) r (ε;η) не змінюється від додавання до ε і η будь-яких постійних (невипадкових величин) або від множення на них;
4) якщо r лежить в таких межах – 1 ≤ (ε;η) ≤ 1, то коли r = –1 або r =1 кореляційний зв’язок замінюється функціональним:
 |
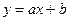
Причому, +1 чи -1 визначається знаками системи координат;
5) якщо r < 0, то з ростом однієї величини друга спадає, і навпаки, якщо r > 0, то обидві величини зростають або спадають.
Мат. сподівання випадкової величини η при значенні іншої взаємопов’язаної величини ε = x називають умовним математичним сподіванням.
Для дискретних випадкових величин:
і неперервних випадкових величин:
,
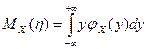де 
- умовна імовірність того, що коли випадкова величина ε = x, то випадкова величина η = y, де y включає в себе всі можливі значення η.
φ 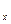(y) – умовна густина імовірності випадкової величини η,коли ε = x.
Очевидно, що 
залежить від x, тобто є функцією x:
і називається функцією регресії випадкової величини η на випадкову величину ε.
Рівняння y = f(x) називається рівнянням регресії.
Розглянемо найпростіший випадок лінійної кореляції між двома випадковими величинами. Причому рівняння регресії випадкової величини ε та випадкової величини η матиме вигляд:
,
де x - значення випадкової величини ε;
a – математичне сподівання випадкової величини ε;
b – математичне сподівання випадкової величини η;
ρ(η/ε) – коефіцієнт регресії випадкової величини ε на η;
,
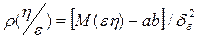де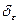 
- стандартне відхилення ε.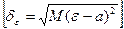 
; 
Коефіцієнт кореляції:
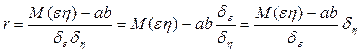
Звідки:
§ 1.5. Математична статистика
Розв’язок будь-яких задач з використанням задач теорії ймовірності в тих випадках, коли використовується їх статистичне визначення, неможливий без отримання відповідного статистичного матеріалу, що базується на великій кількості дослідів.
При цьому виникають задачі, зв’язані з правильною обробкою статистичних матеріалів і надання їм форми, зручної для наступного використання методів теорії ймовірностей.
Розділ теорії ймовірностей,який займається регістрацією, обробкою і аналізом статистичних матеріалів називається математичною статистикою.
Основною метою обробки і аналізу статистичної інформації є виявлення законів розподілу і числових характеристик випадкових величин.
Всі задачі математичної статистики можна розділити на три групи:
1) визначення закону розподілу за статистичними даними (вирівнювання статистичних даних з ростом кількості дослідів); обмежене число дослідів, яке дає можливість визначити F(x), φ(x); об’єм даних повинен бути як можна більшим;
2) перевірка правдоподібності гіпотез. Необхідно визначити, що розбіжність значень густини (функції) теоретичної і статистичної визнані випадковими величинами (через обмежене число дослідів). Якщо малоймовірно, що розбіжність випадкова,то прийняття гіпотези неможливе;
 | |||
 | |||
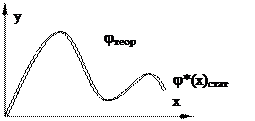3) визначення зв’язку між параметрами розподілу: відомі параметри – невідомий розподіл, і навпаки.
Розглянемо питання про точність визначення статистичної імовірності будь-якої події на основі дослідів або спостереження за схемою незалежних випробувань.
Закон великих чисел (теорема Бернуллі): при необмеженому зростанні числа випробувань імовірність того, що різниця між спостереженою відносною частотою деякої події А, що дорівнює m/n,(де n – число випробувань, m – число появи події) і дійсною імовірністю події Р буде менша будь-якого самого малого числа ε→1, тобто:
Це означає, що при достатньо великій кількості випробувань імовірність похибки в заміні ймовірності випадкової події відносною частотою прямує до нуля, але нескінченно велика кількість випробувань нездійснена практично і доводиться обмежуватись деяким великим числом випробувань.
При цьому похибка у визначенні ймовірності за відносною частотою також є випадковою величиною, яка має ту чи іншу ймовірність.
Інтегральна гранична теорема Муавра – Лапласа дозволяє визначити ймовірність тієї чи іншої похибки.
Згідно з нею:
,
де a і b – довільні числа;
Р – дійсна ймовірність події; q=1–p.
Один із наслідків цієї теореми:
, (*)
де m/n – відносна частота появи події;
ε – довільне число;
Φ(x) – інтеграл імовірності (функція Лапласа).
Це дає можливість визначити наближено ймовірність похибки ε в оцінці ймовірності події р. При визначенні статистичної ймовірності будь-якої події можуть виникнути три задачі, розв’язок яких базується на використанні (*).
Нехай, наприклад, подією буде аварійний вихід в годину вечірнього максимуму енергосистеми будь–якого агрегата. Тоді число випробувань буде число днів спостереження n, а число появи події – число днів, коли даний агрегат знаходиться в період максимуму в аварійному стані.
Задача 1
Знайти найменше число випробовувань, при якому різниця відносної частоти m/n і ймовірності р не перевищує заданої величини ε з надійністю β.
Розв’язок
.
За таблицею знаходимо аргумент 
.
Задача 2
Знайти ймовірність того, що відхилення відносної частоти m/n від імовірності р буде менша деякої величини ε, коли число випробувань рівне n.
Розв’язок
,
за знайденим значенням α знаходимо з таблиці β.
Задача 3
Знайти максимальне відхилення відносної частоти події m/n від його імовірності p при числі випробувань n і заданій імовірності β.
Розв’язок
Враховуючи, що 
, знаходять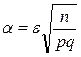 
.
Звідси знаходимо ε:
.
