Одним з найпростіших випадкових процесів є послідовність подій або потік однорідних випадкових подій, тобто випадкове чергування цих подій. Прикладами таких процесів в техніці можуть бути виклики абонентів АТС.
Найпростішим потоком однорідних подій називається потік, що володіє трьома властивостями: стаціонарністю, відсутністю наслідків і ординарністю.
За величину, що характеризує даний потік, приймемо ймовірність того, що за деякий інтервал часу τ (від а до а+τ) відбудеться k однорідних подій і позначимо її 
.
Стаціонарність процесу полягає в тому, що значення не залежить від а - початку даного інтервалу, тобто імовірнісні характеристики потоку не залежать від часу τ може бути будь-яке число подій від 0 до ∞, то:
.
Відсутність наслідків означає, що не залежить від подій, що відбувалися до початку інтервалу. Значить імовірність того, що за інтервал відбудеться саме k подій (за умови, що до початку інтервалу відбулось деяке число подій), дорівнює безумовній імовірності . Таким чином проходження процесу в інтервалах часу, що не перетинаються, незалежне.
Ординарність потоку показує, що імовірність виникнення двох і більше подій за інтервал τ прямує до нуля при τ→0. Якщо позначимо імовірність виникнення двох і більше подій за інтервал τ через Ψ(τ), то ординарність означає, що Ψ(τ)→0 при τ→0.
.
Таким чином, за короткий інтервал часу виникнення двох подій має малу імовірність того, що практично неможливо.
Для характеристики потоку однорідних подій достатньо визначити значення функції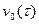 
і всі значення (k =1, 2, 3...).
Загальний вираз імовірності:
,
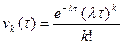де λ- інтенсивність потоку подій, що дорівнює границі відношення числа подій за інтервал τ до величини інтервалу при його безмежному спаданні.
При k =0; k =1; k=2:
, 
, 
.
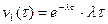Ці ймовірності відповідають розподілу Пуассона, але з параметром, що залежить від тривалості інтервалу τ.
Отже, математичне сподівання числа подій за інтервал τ дорівнює λτ при будь-якому значенні τ. Отже, λ являє собою математичне сподівання числа подій за одиницю часу.
Оцінка інтенсивності потоку, звичайно, може бути отримана лише з тривалих статистичних спостережень за потоком.
Розділ теорії ймовірності, що розглядає закономірності потоків випадкових однорідних подій, називається теорією масового обслуговування.
§ 2.1. Елементи математичної основної теорії надійності
Елементи і системи, з яких вони складені, можуть перебувати у справному й несправному стані.
Несправністю називають всяку невідповідність елемента чи системи одній чи декільком вимогам, яким вони повинні відповідати.
Подія, яка полягає у переході від справного стану в несправний, називається відмовою, чи виходом з ладу.
Основною мірою надійності елемента чи системи є імовірність безвідмовної роботи протягом заданого часу в певних умовах, яку називають надійністю елемента чи системи.
Тобто надійність визначається як імовірність того, що час T безвідмовної роботи елемента чи системи буде більшим заданого часу t, тобто р(t)= ім. (T>t).
Здатність елементів і системи виходити з ладу (відмовляти в роботі) називається ненадійністю, яка визначається імовірністю того, що час T безвідмовної роботи елемента чи системи буде меншим заданого часу, тобто q(t)= ім. (T<t).
Ненадійність є функцією розподілу імовірності часу безвідмовної роботи елемента чи системи.
р(t)+q(t)=1.
Для малих значень t значення р(t) близьке до 1, тому для характеристики надійності користуються поняттям густини розподілу (імовірності) часу безвідмовної роботи:
φ(t)= 
.
|
|
|
|
 |
Середнім часом роботи елемента (системи) називають
математичне сподівання часу його роботи:
.
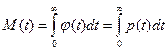Це означає, що час роботи дорівнює площі поверхні, обмеженої кривою р(t) і віссю часу (див. мал.).
Частота відмов дорівнює кількості відмов, які виникають за одиницю часу, віднесеній до кількості випробувань елементів. Числово вона дорівнює густині розподілу часу безвідмовної роботи.
Інтенсивність (небезпека) відмови дорівнює відношенню елементів, які виходять з ладу за одиницю часу до загального числа елементів, що працюють у даний момент часу.
Вона характеризує ступінь надійності елемента (системи). Криву інтенсивності відмов можна розбити на три ділянки. В початковий момент інтенсивність зростає, що зумовлено наявністю дефектних елементів, які виходять з ладу.
Період 
характеризується приблизно постійною інтенсивністю відмов. Починаючи з моменту часу 
, інтенсивність відмови зростає за рахунок старіння елементів.
Час безвідмовної роботи елемента чи системи (при λ=const) можна визначити з виразу:
p(t)= exp (-λt)
Середній час роботи елемента при постійній інтенсивності (небезпеці) відмови:
.
При короткочасній роботі надійність визначається:
.
Іноді надійність підлягає нормальному закону розподілу:
.
