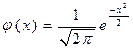Енергетичні системи об’єднують велику кількість різних технічних пристроїв, як генеруючих так і тих що передають електричну енергію, особливо велика кількість пристроїв, які перетворюють електричну енергію. Умови роботи великої сукупності навіть однорідних технічних пристроїв різко відрізняються одні від одних і носять, з точки зору енергетичної системи як цілого, випадковий характер.Так, наприклад, той чи інший пристрій споживачів (ЕД, лампа і т.д.) випадково може бути ввімкненим або ні в електричну мережу, працювати з тим чи іншим степенем віддачі. В результаті накладання таких випадкових подій отримується та чи інша величина попиту потужності в системі, яка залежить від сукупності випадкових подій. Аварійні пошкодження елементів енергосистеми також є випадковими подіями, що виникають в результаті накладання великої кількості несприятливих умов. Лише знаючи імовірні характеристики випадкових подій, можна вірно визначати сумарну величину попиту, величину необхідного резерву потужності і т.д.
В енергетиці важливо при розв’язку задач оптимізації, тобто при виборі оптимальних рішень, використовувати імовірнісні характеристики випадкових явищ. Так, наприклад, надійність електропостачання залежить від багатьох випадкових подій. Щоб вибрати оптимальну схему, яка б відповідала мінімуму затрат, необхідно оцінити не лише затрати на створення тієї чи іншої системи, але й імовірні збитки від перерв електропостачання для кожної з розглядуваних схем.
Два методи визначення імовірності: класичний і статичний.
Класичне визначення можливе лише в тому випадку, якщо досліджувані випадкові події створюють повну групу попарно несумісних і рівноможливих подій. Події, що утворюють таку групу, називаються випадками.
В цьому випадку імовірність вважають рівною відношенню числа випадків, коли дана подія відбулась, до загального числа можливих випадків:
.
На практиці загальну кількість випадків, а також кількість бажаних випадків підрахувати неможливо. Крім того, припущення про рівну можливість тих чи інших подій групи не завжди вдається довести. Тому в енергетиці доводиться користуватися статистичним визначенням імовірності.
Статистичне визначення імовірності базується на статистичних матеріалах. Спостерігаючи будь-яку випадкову подію або здійснюючи випробовування, можна визначити відносну частоту виникнення даної події. При достатньо великій кількості випробувань відносна частота виникнення події коливається відносно деякої постійної величини, яка називається статистичною імовірністю даної події.
Незалежними називаються події А і В, коли виникненняоднієї з них не впливає на імовірність виникнення другої. Залежними – навпаки.
В енергетиці доводиться вивчати імовірності не простих подій, а складних випадкових подій, які є комбінаціями ряду простих. Визначення імовірності складних подій через відомі імовірності простих випадкових подій виконується на базі законів імовірності складних подій:
1) імовірність виникнення хоча б однієї з двох випадкових незалежних і несумісних подій А і В дорівнює сумі імовірностей цих подій:
2) імовірність виникнення хоча б однієї з двох незалежних і сумісних подій А і В:
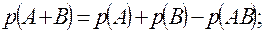
3) імовірність одночасного виникнення двох несумісних подій А і В дорівнює нулю:
4) імовірність одночасного виникнення двох незалежних і сумісних подій дорівнює добутку їх імовірностей:
сума імовірностей протилежних подій дорівнює одиниці:
;
5) імовірність протилежної події:
.
Наприклад: аварійні пошкодження обладнання, приладів – випадкові події. При великій кількості агрегатів на електростанції і елементів мережі пошкодження одних може поєднуватись з пошкодженням інших. Виникає задача визначення імовірності одночасного пошкодження двох, трьох і більше агрегатів. Часом необхідно визначити імовірність того, що пошкоджень нема, так як ця величина характеризує надійність електропостачання. Ці задачі виникають за необхідності вибору оптимального плану розв’язку. В усіх випадках окремі пошкодження розглядаються як випадкові події і імовірність визначається для кожного з них як статична імовірність. Для оцінки імовірностей залежних випадкових подій вводиться поняття умовної імовірності.
Умовною імовірністю події А по події В називається імовірність події А, якщо відбувається подія В; 
.
Основні закони для взаємозв’язаних випадкових подій:
1) умовна імовірність А по В при їх сумісництві і взаємозалежності дорівнює відношенню імовірності одночасного настання подій А і В до імовірності події В.
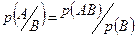, причому 
2) імовірність одночасного настання двох взаємозв’язаних і сумісних подій:
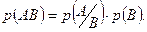
Взаємозв’язаними є пошкодження окремих фаз ЛЕП.
При великій кількості однотипних агрегатів в електричній системі імовірності пошкодження різного числа агрегатів можуть бути визначені за біноміальною формулою імовірності для схеми незалежних випробовувань (формула Бернуллі).
(*)
Вираз (*) називається формулою біноміального розподілу, причому
.
Випадкові величини
До випадкових величин в електроенергетиці відносяться такі важливі параметри режиму, як попит електричної потужності і енергії, відхилення частоти і напруги в електричних мережах від номінальних значень, потужність агрегатів в аварійному ремонті і т.п. Значення закономірностей зміни цих випадкових величин необхідне як при проектуванні, так і при експлуатації енергетичних систем. Основою для їх визначення є статистичний матеріал і методи теорії імовірності.
Випадкові величини поділяються на дискретні і неперервні.
Дискретна величина набуває лише дискретних значень, наприклад, число агрегатів, що вийшли аварійно з роботи. Це число в обмеженому інтервалі є кінечним.
Неперервні величини змінюються неперервно, тобто навіть в обмеженому інтервалі кількість їх значень безмежна.
Для дискретних величин розподіл імовірностей різних їх значень може бути заданий у вигляді таблиць: в верхньому рядку – значення, яких набуває дискретна випадкова величина; в нижньому – імовірність відповідних її значень.
x 
| x  
| x 
| 
| x 
|
| p
| p
| p
|
| p
|
Для неперервних величин неможливо представити закон розподілу у вигляді таблиці, так як число значень таких випадкових величин безкінечне навіть в обмеженому інтервалі.
Подія – прийняття випадковою величиною певного значення.
Для кількісної оцінки імовірностей як неперервних, так і дискретних випадкових величин вводять функцію розподілу F(x), яка за визначенням дорівнює імовірності того, що дана випадкова величина η потрапитьв інтервал значень від - ∞ до деякого значення x.
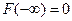і 
Щоб знайти функцію розподілу дискретних випадкових величин, можна використовувати таблиці, виконуючи сумування імовірностей зліва направо.
Для неперервних випадкових величин функція розподілу задається аналітично або графічно.
Імовірність попадання випадкової величини в певний інтервал значень (
; 
),якщо відомі значення F() F(): 
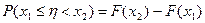
Закон розподілу неперервних величин може бути заданий густиною розподілу ймовірностей φ(x), яка є похідною від функції розподілу випадкової величини х:
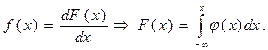
Імовірність попадання випадкової величини η вінтервал від до :
Розподіли випадкових величин
В енергетиці широко використовуються випадкові величини зі слідуючими розподілами: рівномірне, просте нормальне, загальне нормальне, біноміальне, по закону Пуассона.
Рівномірний розподіл знаходить використання при описах деяких випадкових величин в задачах оперативного керування. Так, положення робочої точки регулятора швидкості турбіни всередині зони невідчутності визначається рівномірним розподілом. Крім того, рівномірний розподіл є основою методу статистичних випробувань (Монте-Карло), що використовується при визначенні резерву потужності, відмови в спрацюванні автоматики і т.п.
Нормальний розподіл – як простий, так і загальний використовується при виявленні похибок прогнозування навантаження споживачів і являється гарною математичною моделлю випадкових коливань навантаження, що складаються з великої кількості навантажень окремих ЕП, вмикаємих і вимикаємих від мережі у випадкові моменти часу. Накладаючись одне на одне, ці випадкові збудження формують процес навантаження з розподілом близьким до нормального.
Властивості нормального розподілу.
В першому наближенні ЕЕС можна вважати лінійним динамічним об’єктом. Лінійні об’єкти, на вході яких діє збурення з кінцевомірним нормальним законом розподілу, зберігають нормальний закон і для вихідних параметрів режиму (частота, перетоки потужності і т.д.)
В теорії імовірностей доведено, що якщо навіть окремі випадкові фактори взаємодії мають розподіл, відмінний від нормального, то результуюча взаємодія буде мати розподіл, близький до нормального. Головне, щоб цих факторів було багато.
Параметри режиму з нормальним законом розподілу володіють ще однією властивістю. Оптимальні процедури обробки цих параметрів в задачах прогнозу і фільтрації виявляються лінійними, тобто дуже простими.
Простий нормальний розподіл:
