Нехай в результаті досліду отримані деякі дані, що подані у вигляді таблиці. Потрібно знайти оцінки математичного сподівання, дисперсії і нормальної кореляційної функції. Перевіримо гіпотезу про те, що дана функція є стаціонарною. Так як при розв’язку практичних задач дослідних даних (реалізацій випадкових функцій) є обмежене число, то це може привести до того, що теорія статистичної перевірки гіпотез, яка базується на достатньо великій кількості спостережень, не підтвердить гіпотези про стаціонарні функції, хоча насправді є всі підстави вважати таку гіпотезу справедливою.
Основною ознакою стаціонарності випадкової функції є однорідність протікання процесу в часі.
Випадковий процес в будь-якій динамічній системі починається з нестаціонарної стадії – перехідного процесу, після затухання якого система переходить в усталений режим, і тоді процеси, які відбуваються в системі, можуть бути описані стаціонарними функціями.
Таким чином, вважатимемо випадковий процес стаціонарним, а зміни математичного сподівання і дисперсії віднесемо на рахунок спотворень. Сумуючи по стовпцях і розділивши суму на n – число реалізацій, і знайдемо наближено залежність середніх арифметичних значень від проміжку часу t.
| 
| … | 
|
| 
| … | 
|
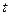
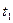
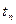
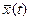
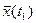
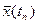
Для отримання оцінки математичного сподівання обчислюють середнє арифметичне із середніх арифметичних координат випадкового процесу:
.
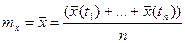Знайшовши оцінку дисперсії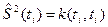 
і їх середнє арифметичне, знайдемо оцінку дисперсій для стаціонарної функції:
.
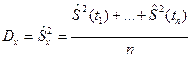Оцінка стандартного відхилення:
.
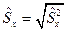Обчислимо нормовану кореляційну функцію. Для стаціонарного випадкового процесу кореляційна функція залежить від величини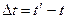 
. Отже, при Δt = const кореляційна функція є сталою. Дисперсія стаціонарної функції не змінюється з часом, тому й нормована кореляційна функція є сталою при Δt = const.
Знайшовши по реалізаціях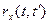 
і звівши їх в таблицю, зможемо знайти оцінку нормованої кореляційної функції.
|
| 
| … |
| |
|
| 
| 
| … | 
|
|
| 
| 
| … | … |
… 
| … | … | … | … |
|
| … | … | 
|
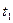
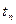
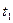
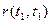
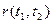
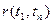
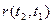
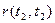
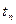
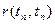
Постійному значенню Δt відповідає головна діагональ (Δt 
=0) і паралелі цієї діагоналі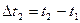 
. Знайшовши середнє оцінок значень нормованої кореляційної функції, запишемо отримані значення у вигляді таблиці.
| 
| … | 
|
| 
| … | 
|
; 
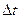
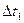
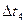
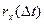
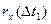
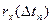
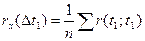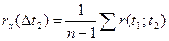
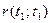- показує початок діагоналі.
Після визначення нормованої кореляційної функції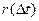 
і побудови її графіка потрібно її апроксимувати простим аналітичним виразом, який повинен відображати найбільш характерні властивості графіка функції і згладжувати випадкові коливання при великих Δt, тобто в точках, отриманих осередненням невеликого числа даних і тому ненадійних. Найбільш часто використовують такі апроксимальні вирази:
 |  | ||
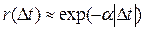
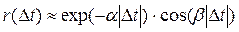
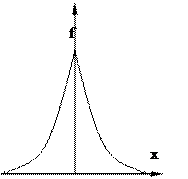