Нестаціонарні процеси, наприклад, в задачах оперативного керування можна віднести до двох типів: адитивні і мультиплікативні.
До першого типу відносяться процеси виду x(t)=y(t)+a(t), де y(t) - стаціонарний випадковий процес; a(t) - детермінована функція (a(t) 
).
Такі процеси також називаються нестаціонарними по математичному сподіванню.
Прикладом таких процесів є такі параметри режиму, як перетоки активної потужності, частота і т.п.
До другого – процеси виду:
x(t)=y(t)·a(t) або x(t)=y(t)·z(t),
де y(t), z(t) - деякі випадкові процеси; a(t) - детермінована функція. 
Прикладом може бути добова реалізація графіка енергобалансу потужності крупного енергооб’єднання.
Обчислення оцінки математичного сподівання ергодичного стаціонарного випадкового процесу за формулою (1*) можна розглядати, як згладжування її реалізації, отриманої в результаті досліду.
Математичне сподівання нестаціонарного випадкового процесу також можна визначити згладжуванням однієї реалізації, якщо отримана в результаті досліду реалізація випадкового процесу є достатньої тривалості і добре являє всю сукупність можливих реалізацій. Для згладжування використовується метод ковзаючої середньої, який полягає в тому, що за згладжене значення функції в будь-якій точці t приймають середнє значення в деякому інтервалі з центром в цій точці. При зміні t інтервал ковзає вздовж осі t.
Розіб’ємо відрізок [0;T] реалізації випадкового процесу на рівні ділянки точками 
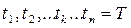. Для визначення згладженого значення функції в точці 
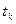виділимо з множини точок 
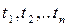таку підмножину 2p+1 точок, тобто множину точок:
,
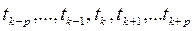в якій центральною точкою є точка 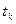. Згладжене значення (значення ковзаючої середньої (2р+1)-го порядку в точці :
.
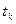Аналогічно можна обчислити згладжені значення в точках 
.
Чим більший інтервал, тим сильніше згладжування, але при дуже великому інтервалі згладжується саме математичне сподівання. Тому інтервал вибирається так, щоб при будь-якому розміщенні його всередині відрізку [0;T] реалізація випадкового процесу мала на ньому достатньо велику кількість коливань і в той же час щоб математичне сподівання випадкового процесу на інтервалі можна було б рахувати приблизно лінійним.
Оцінка кореляційної функції:
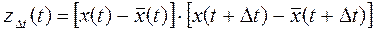
значення Δt фіксується; x(t) і 
- згладжуючи реалізація на відрізках [0;T-Δt], [Δt;T].
Нехай згладжування реалізації проводилось ковзаючої середньою (2р+1)-го порядку. Розіб’ємо відрізок запису реалізації випадкового процесу на рівні проміжки довжиною h точками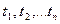 
=Т. Оцінкою значення кореляційної функції 
в точці Δt = m h, де m=0; 1; 2... n є ковзаюча середня, обчислена за наступною сукупністю чисел:
.....................................................................................
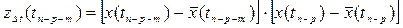
1.7 Контрольні запитання
1. Чому електроенергетичні системи потребують застосування теорії ймовірностей?
2. Сформулюйте теорему додавання та множення ймовірностей.
3. Як виглядає формула повної ймовірності?
4. Яким законам розподілу ймовірностей підпорядковуються дискретні випадкові величини в електроенергетиці?
5. Які закони можуть описувати неперервні випадкові величини в електроенергетиці?
6. Які числові характеристики застосовують для оцінки окремих особливостей випадкових величин?
7. Опишіть методику оцінки збитків за рахунок відхилення напруги приймачів.
8. У чому полягає методика визначення оптимального числа резервних агрегатів?
9. Сформулюйте теореми Чебишева і Маркова про середнє арифметичне спостережених значень.
10. Як застосовується теорема Бернуллі при розв'язуванні практичних задач?
11. Що являє собою простий статистичний ряд, статистична функція розподілу? Як будується гістограма?
12. За якими формулами обчислюють статистичне математичне сподівання, статистичну дисперсію, коефіцієнт кореляції?
13. Як використовується критерій згоди Колмогорова в задачах електроенергетики? Наведіть приклад.
14. Що називається довірчим інтервалом та довірчою імовірністю?
15. Які властивості мають ергодичні випадкові функції?
16. Що являє собою ентропія і в чому полягає теорема додавання ентропій?
17. Що розуміють під методом Монте-Карло, в чому його суть?
18. Визначте поняття надійності.
19. Як обчислюють інтенсивність відмови?
20. Як умови сполучення елементів впливають на надійність системи.
