, де λ- const.
Цей закон часто називають законом рідкісних явищ, так як при малих p і q імовірностях різних значень випадкових величин за біноміальним законом розподілу близьке до аналогічних імовірностей розподілу за Пуассоном.
Числові характеристики випадкових величин.
Через відсутність відповідних статистичних матеріалів не завжди можна задати таблиці розподілу імовірностей для дискретних випадкових величин або функції розподілу і густини розподілу імовірностей для неперервних випадкових величин.
В багатьох випадках достатньо знати числові характеристики випадкових величин, до числа яких відносяться математичне сподівання, дисперсія, стандартне відхилення і моменти випадкових величин.
Випадкова величина може набувати різних значень, тому важливо знати її середнє значення.
Для оцінки середнього (в імовірному змісті) значення випадкової величини вводиться поняття математичного сподівання, яке являє собою дійсно середнє значення випадкової величини, що визначається з врахуванням різних імовірностей окремих значень.
- для дискретних випадкових величин.
Властивості математичного сподівання:
M (С) = С,
М (Сη) = С·М (η),
М (α+ 
) =М (α) + М (β),
М (αβ) = М (α)·М (β) – для незалежних випадкових величин.
Крім математичного сподівання необхідно, знати наскільки відхиляється випадкова величина від свого математичного сподівання. Якщо ці відхилення малі, то математичне сподівання добре являє випадкову величину; якщо ж розсіяння значень випадкових величин великі, то одне математичне сподівання вже не характеризує випадкову величину.
За міру відхилення випадкової величини від її математичного сподівання приймають величину, що дорівнює математичному сподіванню квадрата відхилення випадкової величини від її математичного сподівання, яку називають дисперсією.
.
Середнє квадратичне або стандартне відхилення випадкової величини:
,
,
.
Властивості:
1. 
.
2. 
.
3. 
.
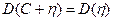4. 
, де ε,η – незалежні випадкові величини.
5. Дисперсія середнього арифметичного від ряду випадкових n величин з однаковою дисперсією в n раз менша дисперсії кожної з них.
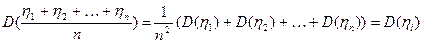
Рівномірний розподіл:
; 
; 
.
Простий нормальний розподіл:
; 
; 
.
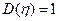Загальний нормальний розподіл:
; 
; 
.
Біноміальний розподіл:
1) якщо випадкова величина представляться у вигляді числа подій m:
; 
; 
;
2) якщо випадкова величина являється відносною частотою m/n, то:
; 
; 
.
Розподіл Пуассона:
.
Моменти.
Найбільш загальною формою характеристики випадкових величин є момент.
Моментом n -го порядку випадкової величини називається математичне сподівання n -го ступеню її відхилення від деякої константи С:
.
Якщо С=0, то момент називається початковим; якщо С=М(η) – центральним.
Математичне сподівання – початковий момент першого порядку, дисперсія – центральний момент другого порядку.
.
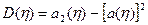Центральний момент першого порядку дорівнює нулю.
Центральний момент третього порядку характеризує коефіцієнт асиметрії:
; 
.
Центральний момент четвертого порядку – коефіцієнт крутизни.
.
В енергетиці інколи являє інтерес визначення не дисперсії D(η), тобто квадрату відхилення від математичного сподівання, а моменту 2-го порядку відносно деякої величини С, тобто математичного сподівання квадрату відхилення випадкової величини від константи С.
;
або 
; 
.
