Системы линейных однородных уравнений

Определение 7.

Система m линейных уравнений с n неизвестными называется однородной, если свободные члены равны нулю.

. (7)

Очевидно!!!

1. Значения - решение системы (7). Следовательно, однородные системы совместны. Матрицы А ~ В,так как они отличаются нулевым столбцом, т. е. и по теореме Кронекера – Капелли система совместна.

2. Если , решений множество и нулевое будет среди них.

Для отыскания ненулевых решений (7) берут любые уравнений, таких, что коэффициенты образуют . Из этих уравнений r неизвестные также выражаются через остальные , называемые свободными.

Если рассматривать значения свободных переменных как вектор , то очевидно, что можно сформировать линейно-независимых решений, принимая значения свободных переменных в соответствии с

. (9)

Определение 8.

Совокупность решений, полученная на основе полной линейно-независимой системы значений свободных переменных, называется фундаментальной.

ПРИМЕР 3:

, .

Это однородная система (, ). Примем свободных неизвестных. Пусть - свободные. Выразим оставшиеся переменные через свободные переменные. Вычтем из второго уравнения удвоенное первое и получим

.

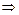
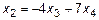Из третьего уравнения вычтем первое, умноженное на 6, и получим

.

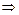
Тогда система решений имеет вид 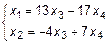. Примем значения такие, что , и вектор решения . Примем 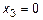, и вектор решения . Поскольку вектора и линейно независимы, множество решений будет определяться линейной комбинацией этих векторов .

4. Метод Жордана – Гаусса

Поскольку , то, если путем элементарных преобразований свести матрицу A к единичной матрице , получим . То есть для решения системы необходимо путем элементарных преобразований свести расширенную матрицу к единичной диагональной. Тогда столбец свободных членов примет значения, соответствующие решению

~ ~

~ .

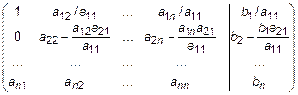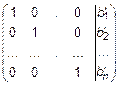Таким образом, последний столбец соответствует решению системы линейных уравнений . Если в системе уравнений , то принимаются определенные значения свободных переменных в соответствии с (9). Полученные коэффициенты добавляются к столбцу свободных членов и решения находятся по описанному выше алгоритму.

ПРИМЕР 4.

, ~

~ ~ ~ ~ ~ .

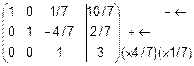Ответ сходится с решением методом Крамера.

 

Заключение

В лекции введено понятие «система линейных уравнений». Для правильного ее решения важно понимать и уметь вычислять определитель и ранг обычной и расширенной матриц. При возникновении затруднений в этом вопросе рекомендуется вернуться к двум прошлым лекциям. Видно, что методов решений множество. Далеко не все здесь представлены. Так метод матриц компактен, но не нагляден. Методы Крамера и Жордана – Гаусса более наглядны, однако необходимо большое количество операций при вычислении. За счет однотипности операций метод Жордана – Гаусса легче переводится на языки программирования. Известный еще со школы метод непосредственной подстановки наиболее нагляден и прост, но и он требует наибольшее количество вычислений, и переложить его на язык программирования практически невозможно. Важно отметить необходимость понятия «фундаментальное» решение. Отметим следующее:

- ранги обычной и расширенной матриц могут быть не равны, и система в этом случае не совместна;

- в случае их равенства решение может быть единственным (квадратная матрица) или их может быть множество (прямоугольная матрица);

- в матричном методе используется обратная матрица;

- в методе Крамера используются дополнительные определители;

- в методе Жордана – Гаусса необходимо свести основную матрицу к единичной;

- в однородных уравнениях правые части равны нулю;

- с помощью фундаментального решения системы однородных уравнений можно получить множество решений.

Литература

1. Баврин И.И. Высшая математика. – М.: Просвещение, 1980.

2. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Физматлит, 2001.

3. Шипачев В.С. Основы высшей математики. – М.: Высшая школа,1998.

4. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Наука, 1989, - 659 с.

Лекция 11