Определение 7.
Суммой матриц А и В называется такая матрица, каждый элемент которой равен сумме соответствующих элементов матриц А и В.
Пусть 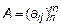 и
и 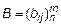 . Тогда
. Тогда 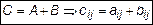 .
.
2.2. Справедливы свойства операции сложения
1. 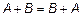 ;
;
2. 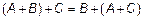 ;
;
3. Существует 0-матрица, все элементы которой – нули: 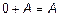 ;
;
4. Существует 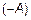 – противоположная матрица такая, что
– противоположная матрица такая, что 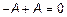 .
.
Произведением матрицы на число называется матрица, все элементы которой равны произведению каждого элемента матрицы на это число.
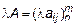 ,
, 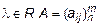 .
.
2.3. Свойства операции умножения матрицы на число
1. 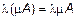 ,
, 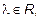 ,
, 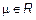 ;
;
2. 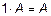 ;
;
3. 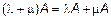 ;
;
4. 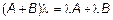 .
.
Вывод!!! Все матрицы одного порядка образуют линейное пространство – 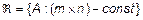 .
.
2.2. Нелинейная операция, произведение матриц
Определение 9.
Произведением матрицы А порядка  на матрицу В порядка
на матрицу В порядка 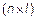 называется матрица С порядка
называется матрица С порядка 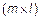 , любой элемент которой равен сумме попарных произведений элементов i-й строки матрицы А на соответствующий элемент j-го столбца матрицы В
, любой элемент которой равен сумме попарных произведений элементов i-й строки матрицы А на соответствующий элемент j-го столбца матрицы В
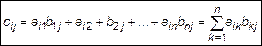 . (2)
. (2)
ПРИМЕР 1.
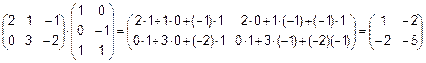 Замечание!!!
Замечание!!!
Можно умножать лишь те матрицы, у которых совпадает число столбцов первой матрицы с числом строк во второй. Произведение матриц, в общем, не коммутативно – 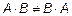 .
.
3. Обратная матрица
Определение 10.
Матрица, все элементы которой, расположенные вне главной диагонали, равны нулям, называют диагональной
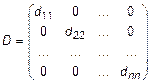 .
.
Определение 11.
Диагональная матрица, у которой все элементы главной диагонали равны 1, называют единичной
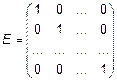 .
.
Очевидно!!! 1. 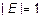 ; 2. Для квадратной матрицы
; 2. Для квадратной матрицы 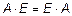 .
.
Определение 12.
Если для A существует 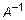 , то матрица А называется обратимой. Матрица
, то матрица А называется обратимой. Матрица 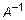 называется обратной матрицы
называется обратной матрицы 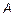 , если справедливо равенство
, если справедливо равенство
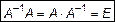 . (3)
. (3)
Теорема 1
Если матрица А не вырождена, то она обратима, причем
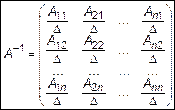 . (4)
. (4)
Доказательство.
По определению с учетом теоремы Лапласа 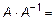
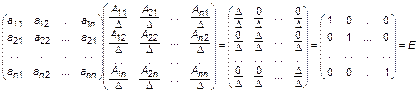
ПРИМЕР 2.
Дано 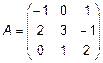 . Найти
. Найти 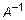 .
.
1) 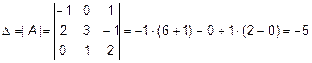 .
.
2) Найдем алгебраические дополнения и подставим в (4):
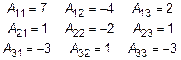
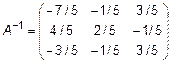 .
.
4. Ранг матрицы
Определение 13.
Минором k-го порядка матрицы А называется определитель, составленный из элементов этой матрицы, стоящих на пересечении любых k строк и k столбцов этой матрицы. Обозначается 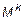 .
.
ПРИМЕР 3.
Для матрицы 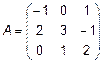 соответствуют миноры:
соответствуют миноры: 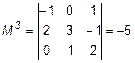 ,
, 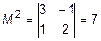 ,
, 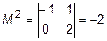 .
.
Определение 14.
Рангом матрицы называется наивысший порядок k минора, отличный от нуля. Обозначается 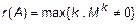 .
.
4.1. Правило нахождения ранга
- Проверяют все миноры первого порядка 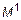 , то есть элементы матрицы.
, то есть элементы матрицы.
- Если 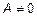 , проверяют все миноры второго порядка
, проверяют все миноры второго порядка 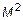 . Если все
. Если все 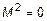 , то ранг матрицы
, то ранг матрицы 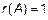 .
.
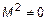 , то проверяют все миноры третьего порядка
, то проверяют все миноры третьего порядка 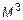 , и т. д. В примере
, и т. д. В примере 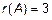 .
.
Определение 15.
Элементарными преобразованиями матрицы называются следующие операции над матрицей:
- перемена мест строк (столбцов);
- умножение всех элементов строк (столбцов) на одно и то же число 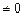 ;
;
- прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число;
- отбрасывание строк (столбцов), состоящих из нулей.
Определение 16.
Если матрица А получена из матрицы В элементарными преобразованиями, то матрицы называются эквивалентными А~В.
Теорема 2
Если матрица А~В, то r (A) =r (B).
Следствие!!!
Ранг матрицы 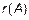 можно искать следующим образом: с помощью элементарных преобразований привести матрицу А к матрице, все элементы которой ниже главной диагонали равны нулям. Тогда ранг матрицы будет равен числу элементов на главной диагонали.
можно искать следующим образом: с помощью элементарных преобразований привести матрицу А к матрице, все элементы которой ниже главной диагонали равны нулям. Тогда ранг матрицы будет равен числу элементов на главной диагонали.
ПРИМЕР 4.

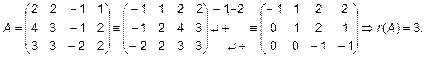 5. Преобразование координат
5. Преобразование координат
Пусть 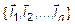 и
и 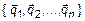 – два произвольных базиса n -мерного линейного пространства R. Поскольку это базисы одного пространства, то каждый базисный вектор
– два произвольных базиса n -мерного линейного пространства R. Поскольку это базисы одного пространства, то каждый базисный вектор 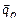 может быть представлен линейной комбинацией векторов
может быть представлен линейной комбинацией векторов 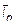
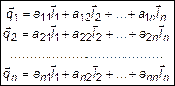 . (5)
. (5)
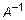 (4).
(4).
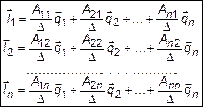 . (6)
. (6)
ПРИМЕР 5.
Даны два базиса в декартовой системе координат 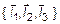 ,
, 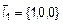 ,
, 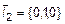 ,
, 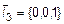 и
и 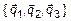 ,
, 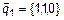 ,
, 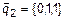 ,
, 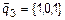 (рис. 1). Определить матрицу перехода из одного базиса в другой.
(рис. 1). Определить матрицу перехода из одного базиса в другой.
Решение. Не трудно заметить, что
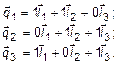
Следовательно, матрица перехода от базиса 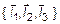 к базису
к базису 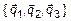 будет иметь вид
будет иметь вид
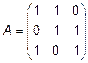 .
.
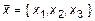 в базисе
в базисе 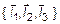 представим в базисе
представим в базисе 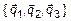 . При этом он будет иметь новые координаты
. При этом он будет иметь новые координаты 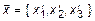 . Представим вектор виде линейной комбинации базисных векторов
. Представим вектор виде линейной комбинации базисных векторов
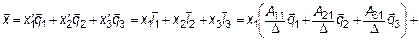
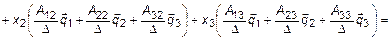
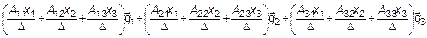 Осюда следует, что преобразование координат осуществляется за счет транспонированной обратной матрицы
Осюда следует, что преобразование координат осуществляется за счет транспонированной обратной матрицы 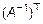 :
:
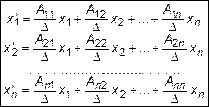 . (7)
. (7)
ПРИМЕР 6.
Представим в исходном базисе 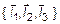 ,
, 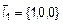 ,
, 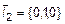 ,
, 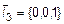 вектор
вектор 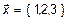 (рис. 1). Переведем эти координаты в другой базис
(рис. 1). Переведем эти координаты в другой базис 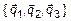 ,
, 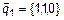 ,
, 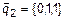 ,
, 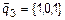 . С учетом предыдущего примера запишем транспонированную обратную матрицу
. С учетом предыдущего примера запишем транспонированную обратную матрицу
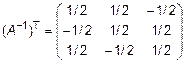 .
.
Тогда новые координаты вектора  получим согласно (7)
получим согласно (7)
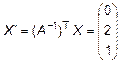 ,
,
где 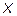 - матрица-столбец координат вектора, то есть в новой системе координат вектор будет представлен как
- матрица-столбец координат вектора, то есть в новой системе координат вектор будет представлен как 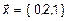 (рис. 1).
(рис. 1).
Заключение
- матрица – это таблица элементов любой природы;
- складываются матрицы поэлементно;
- умножаются матрицы методом «сумма произведений строка на столбец»;
- обратная матрица находится с помощью определителя и алгебраических дополнений;
- транспонированная матрица получается путем «поворота» матрицы;
- ранг матрицы – минор наивысшего порядка, отличный от нуля;
- преобразование базиса осуществляется за счет прямой матрицы;
- обратное преобразование базиса осуществляется за счет обратной матрицы;
- прямое преобразование координат осуществляется за счет обратной транспонированной матрицы.
Литература
1. Ильин В.А., Позняк Э.Г. «Линейная алгебра». – М.: Физматлит, 2001. – 318 с.
2. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Физматлит, 2002.
3. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Наука, 1989. – 659 с.
4. Рыжков В.В. Лекции по аналитической геометрии. – М.: Факториал пресс, 2000. – 208 с.






