Даны две плоскости в отрезках 
и 
. При пересечении этих плоскостей образуется прямая 
, т. е.
.
. (2)
Вывод!!!
Очевидно, что как для плоскости, так и для прямой, проходящей через начало координат, уравнение в отрезках записать нельзя.
ПРИМЕР 1.
. Перейдем к уравнению в отрезках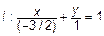 
(рис.5).
3. Уравнение прямой с угловым коэффициентом
Обозначим 
- угол, образованный прямой с положительным направлением оси Ox, 
– угловой коэффициент прямой l, b – отрезок OB, отсекаемый на оси Oy, точка B(0,b) (рис. 6).
Эта точка и определяют единственную кривую на плоскости. Возьмем некоторую текущую точку 
, 
– текущие координаты. Из 
определим 
. То есть 
, откуда получим уравнение прямой с угловым коэффициентом
. (3)
3.1. Переход от общего уравнения прямой к уравнению
с угловым коэффициентом
Разрешим уравнение (1) относительно y. Получим 
, где 
и 
имеют смысл лишь при 
.
Вывод!!!
Уравнение прямой с угловым коэффициентом можно записать только для прямой не параллельной оси 
.
4. Уравнение прямой,
проходящей через заданную точку в заданном направлении
Дано: 
и – угловой коэффициент к прямой l. Составим уравнение этой прямой. В уравнении 
неизвестно b. Поскольку точка , то ее координаты удовлетворяют уравнению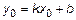 
, откуда получим
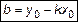. (4)
Тогда уравнение прямой будет иметь вид 
, откуда
. (5)
ПРИМЕР 2.
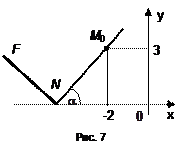Даны точка 
и угол падения луча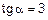 
. Составить уравнение падающего и отраженного лучей. Изобразим это на рис. 7. Обозначим прямую падающего луча 
, а отраженного – 
. Для уравнения используем (5): 
или 
. Определим точку пересечения этой прямой с осью 
: 
или 
, откуда 
. То есть точка 
. Определим для прямой угловой коэффициент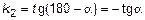 
. Тогда уравнение (5) будет иметь вид 
или 
.
5. Уравнение прямой,
проходящей через две заданные точки
В плоскости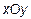 
даны две точк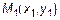и 
и 
. Запишем (5) для точки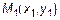
. (6)
Поскольку обе точки лежат на одной прямой, то точка также удовлетворяет (6) 
, откуда
. (7)
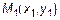, будет иметь вид
.
Разделим обе части равенства на 
и получим уравнение прямой в плоскости, проходящей через две заданные точки
. (8)
6. Угол между двумя прямыми на плоскости
Даны две прямые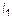 
и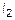 
(рис. 8). Обозначим 
и 
– угловые коэффициенты этих прямых. Обозначим через 
– угол между этими прямыми. В треугольнике 
угол 
– внешний, поэтому 
, откуда 
. Тогда
. (9)
6.1. Условие перпендикулярности прямых
Или 
, 
не существует, следовательно в (9) знаменатель 
, откуда 
или 
, или 
.
6.2. Условие параллельности прямых
, 
, следовательно, в (9) числитель 
, откуда 
или 
.
ПРИМЕР 3.
Даны точки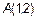 
, 
, 
. Найти уравнение медианы 
и высоты 
. Точка D находится посередине отрезка BC, поэтому ее координаты 
, а уравнение медианы
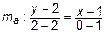или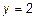 
– прямая, параллельная оси . Для определения уравнения высоты определим ее угловой коэффициент через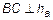 
. Но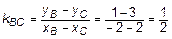 
, тогда 
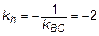. Окончательно уравнение высоты: 
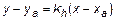. Для 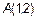имеем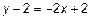 
или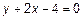 
.
Заключение
В лекции закончено рассмотрение уравнений первого порядка, которые описывают либо плоскость в пространстве, либо прямую на плоскости. Важно запомнить основные уравнения прямой на плоскости и правила перехода между ними. Это пригодится в дальнейшем при изучении темы «Функциональный анализ» и др. Для простоты запоминания рекомендуем обратить внимание на общность подходов при построении уравнений плоскости и прямой. В последующей лекции рассмотрим общие уравнения второго порядка. Отметим следующее:
- прямая на плоскости описывается уравнением первого порядка;
- если прямая проходит через начало координат, то уравнение в отрезках записать нельзя;
- уравнение прямой в отрезках аналогично уравнению плоскости в отрезках;
- угловой коэффициент прямой – это тангенс угла ее наклона относительно оси абсцисс;
- параметр b определяется отрезком, отсекаемым прямой по оси ординат;
- положение прямых и углы между ними определяются их угловыми коэффициентами;
- условие параллельности и перпендикулярности прямых аналогичны этим же условиям для плоскостей.
Литература
1. Бермант А.Ф. и др. Краткий курс математического анализа. – М.: Высшая школа, 2001.
2. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Физматлит, 2002.
3. Шипачев В.С. Основы высшей математики. - М.: Высшая школа,1998.
Лекция 14
Кривые второго порядка
Линия и ее уравнения
Окружность и ее уравнения
Эллипс
4. Исследование формы и расположения эллипса по его каноническому виду
Цели занятия: изучить понятие кривых второго порядка; расширить школьные знания об окружности; изучить правила построения и свойства эллипса; научиться приводить кривые второго порядка из общего в канонический вид.
Роль и место лекции
Общие сведения о понятиях окружности и эллипса известны из школьного курса математики. Многие процессы в окружающем мире подчинены уравнениям этих кривых (например, вращение планет). Однако уравнение окружности было введено только в каноническом или явном виде, а уравнение эллипса не изучалось. В лекции представлены общее и каноническое уравнения эллипса и окружности, полученные на основе классических определений. Более широко эти вопросы будут рассмотрены в теме «Квадратичные формы».
Линия и ее уравнение
Определение 1
Геометрическое место точек – это совокупность точек, обладающих общим свойством. Общее свойство точек линии выражается уравнением линии.
Определение 2
Уравнением линии называется такое уравнение, которому удовлетворяют координаты любой точки этой линии и не удовлетворяют координаты точек, не принадлежащих этой прямой.
В 
уравнение функционально имеет вид 
.Алгебраическое уравнение первого порядка относительно x и y (см. лекцию 13)
– это прямая линия на плоскости .
Кривыми второго порядка называют линии, которым соответствует алгебраические уравнения второго порядка:
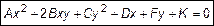, (1)
т. е. окружности, эллипсы, гиперболы, параболы.
Окружность и ее уравнения
Определение 3.
Окружностью называется геометрическое место точек плоскости, равноудаленных от одной точки, называемой центром окружности.
Построим уравнение окружности. Для этого, согласно определению, зададимся центром окружности 
и R – радиусом окружности L (рис.1). Возьмем произвольную точку M (x, y), которая по определению должна принадлежать окружности, следовательно, согласно определению, удовлетворять соотношению
. (2)
Запишем это выражение в координатах
.
Окончательно получим уравнение окружности в каноническом виде
. (3)
2.1. Исследование окружности
1. Если 
, то выражение (3) примет вид 
.
2. Если 
, то выражение (3) примет вид 
.
3. Если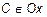 
, то выражение (3) примет вид 
.
Приведем уравнение (3) к общему виду (1). Для этого раскроем скобки и умножим обе части равенства на число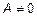 
.
.
Введем обозначения: 
; 
; 
. Подставим эти обозначения и получим уравнение окружности в общем виде
. (4)
- коэффициенты при квадратах текущих координат равны;
- отсутствует член, содержащий произведение текущих координат «
».
2.2. Последовательность перехода от общего
к каноническому виду
Для этого разделим все члены уравнения на коэффициент при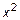 
и выделим полные квадраты с x и y.
ПРИМЕР 1.
Задано уравнение второго порядка: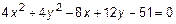 
.
Построить кривую согласно.
Решение.
Поскольку коэффициенты при квадратах одинаковы (=4) и отсутствует член , то можно сказать, что это окружность.
Это окружность (рис. 2) с радиусом R= 4 и центром в точке C (1, -1.5).
Эллипс
Определение 4.
Эллипсом называется геометрическое место точек плоскости, сумма расстояний которых от двух данных точек, называемых фокусами, есть величина постоянная.
Зададим в декартовой системе координат фокусы F 1и F 2(рис. 3). Возьмем произвольную точку M (x, y), которая по определению должна принадлежать эллипсу. Проведем отрезки F 1 M и F 2 M (рис. 3). Согласно определению рассмотрим сумму этих отрезков
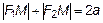, (5)
где 
– некоторое число.
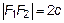, тогда из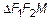 
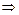
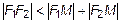
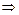
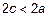или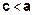 
. Фокусы имеют координаты 
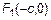и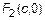 
, причем 
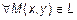– эллипс. Представим выражение (1) в координатах:
.
Перенесем второе слагаемое в правую часть и возведем обе части равенства в квадрат:
.
Раскроем скобки и сократим одинаковые члены равенства в левой и правой частях:
.
Возведем обе части равенства в квадрат:
.
Раскроем скобки и сократим одинаковые члены равенства в левой и правой частях:
,
.
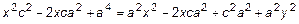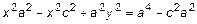Перенесем слагаемые с x и y в правую часть, остальные – в левую. Вынесем за скобки x 2и a 2:
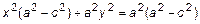. (6)
Отметим, что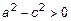 
. Обозначим 
. Запишем выражение (6) через введенные обозначения
, 
. (7)
Выражение (7) есть уравнение эллипса в каноническом виде.
4. Исследование формы и расположения эллипса
по его каноническому виду
Рассмотрим выражение (7) и заметим следующее.
1. Так как текущие координаты входят в уравнение только в квадратах, то эллипс симметричен относительно осей координат – осей симметрии.
Если 
, то 
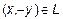и 
.
2. Эллипс L (7) пересекается с осями координат.
a) Пересечение с осью .
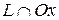, . Из выражения (7) => 
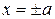. То есть точк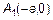и 
и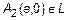 
. Эти точки – вершины эллипса. 
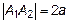– большая ось эллипса. Отметим эти точки на оси (рис. 4).
б) Пересечение с осью .
, 
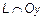. Из выражения (7) => 
. То есть, точки 
и 
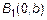. Две точки 
и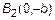 
– также вершины эллипса. 
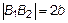– малая ось эллипса. Отметим эти точки на оси (рис. 4).
3. Из уравнения (7) найдем y
. (8)
Для I четверти выражение (8) имеет вид 
. При увеличении x от 0 до a (при x = a y =0) значение y уменьшается от b до 0. Поскольку эллипс симметричен относительно начала координат, то аналогичным образом, сохраняя симметрию, эллипс будет вести себя в остальных четвертях плоскости.
Замечания!!!
1. В частности, при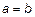 
из (7) имеем 
, 
(окружность – частный случай эллипса).
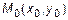, то уравнение эллипса примет вид
. (9)
Определение 5.
Эксцентриситетом называется величина, равная отношению расстояния между фокусами к длине большой оси.
, 
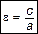. (10)
Чем ближе эксцентриситет к 0 (
), тем более округлую форму эллипс имеет, и наоборот, чем ближе эксцентриситет к 1 (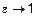
), тем эллипс более вытянут вдоль оси .
Замечание!!!
Последовательность перехода от общего к каноническому виду для эллипса аналогична последовательности перехода для окружности. Для этого вынесем за скобки коэффициент при 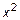и выделим полный квадрат с x. Также вынесем за скобки коэффициент при 
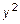и выделим полный квадрат с y.
Заключение
В лекции изучены понятия «окружность» и «эллипс» в общем виде, показано, как строить графики этих функций. По общему виду уравнения второго порядка можно судить о виде кривой. Отметим:
- параметры R, a и b в выражении (3) определяют соответственно радиус и координаты центра окружности;
- от уравнения общего вида к каноническому переходят путем выделения полных квадратов;
- эксцентриситет эллипса ;
- эксцентриситет эллипса определяет его вытянутость;
- окружность – частный случай эллипса;
- фокусы эллипса могут быть найдены из выражения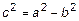 
.
Литература
1. Бермант А.Ф. и др. Краткий курс математического анализа. – М.: Высшая школа, 2001.
2. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Физматлит, 2002.
3. Шипачев В.С. Основы высшей математики. - М.: Высшая школа,1998.
Лекция 15
Кривые второго порядка
Гипербола
