Построим на основании трех векторов 
, 
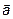и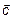 
параллелепипед (рис. 3). Обозначим 
. Модуль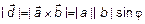 
= 
– площадь основания параллелепипеда. Тогда 
= 
, где 
– высота параллелепипеда, 
– его объем. Окончательно
. (11)
4.3. Смешанное произведение векторов в координатной форме
Запишем векторное произведение через координаты (9). Согласно правилу скалярного умножения векторов получим
. (12)
4.4. Условие компланарности трех векторов
Из геометрического смысла три вектора 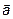, и 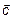компланарны тогда и только тогда, когда объем параллелепипеда, образованного этими векторами, равен нулю. То есть все три вектора лежат в одной плоскости. Следовательно, смешанное произведение этих трех векторов также равно 0. То есть
компланарны 
или 
. (13)
Заключение
В лекции введено понятие квадратной матрицы и ее определителя. В следующей лекции понятие матрицы будет обобщено и показано ее практическое применение для решения систем линейных уравнений. Понятием смешанного произведения векторов и его геометрическим смыслом тема векторной алгебры закрывается. Отметим следующее:
- определитель (число) существует только для квадратных матриц;
- в матрице можно осуществлять линейные операции над строками и столбцами без изменения определителя;
- перемена строк или столбцов меняет знак определителя;
- определители матриц с коэффициентами в виде координат векторов определяют векторные и смешанные произведения;
- направление векторного произведения находится по правилу правого винта;
- модуль векторного произведения – это площадь параллелограмма;
- смешанное произведение векторов – это объем параллелепипеда;
- два вектора параллельны, когда detA=0;
- три вектора компланарны, когда detA=0.
Литература
1. Рыжков В.В. Лекции по аналитической геометрии. – М.: Факториал пресс, 2000. – 208 с.
2. Демидович Б.П. Краткий курс высшей математики. – М.: 2001.
3. Шипачев В.С. Основы высшей математики. – М.: ВШ,1998.
Лекция 9
Матрицы
Общее определение матрицы
Действия над матрицами
Обратная матрица
4. Ранг матрицы
5. Преобразование координат
Цели занятия: расширить понятие «матрица» на общий случай разного количества строк и столбцов; научиться производить действия над матрицами, осуществлять их элементарные преобразования, находить ранг и обратную матрицу; научиться преобразовывать системы координат.
Роль и место лекции
Предлагаемые сведения будут необходимы для восприятия темы «системы линейных уравнений». Понятия ранга матрицы и обратной матрицы являются фундаментальными при решении систем линейных уравнений. Понимание элементарных преобразований матриц указывает на их тесную взаимосвязь с системами уравнений. Матричный математический аппарат непосредственно используется при преобразовании координат и в теории тензорного исчисления.
Общее определение матрицы
Определение 1.
Прямоугольная таблица элементов любой природы, содержащая m строк и n столбцов, называется матрицей порядка 
.
. (1)
Если m=n, то А – квадратная матрица.
Определение 2.
Если определитель квадратной матрицы равен нулю, матрица называется вырожденной, если не равен – не вырожденной матрицей.
Определение 3.
Матрица, содержащая только одну строку, называется матрицей-строкой или строчной матрицей. Ее можно рассматривать как вектор
.
Матрица, содержащая только один столбец, называется матрицей-столбцом или столбцовой матрицей
.
Определение 5.
Матрица 
, полученная из А заменой строк столбцами, называется транспонированной.
; 
.
Определение 6.
Две матрицы одного порядка называются равными, если соответствующие элементы матриц равны.
Матрицы 
и 
равны А=В, если 
.
Действие над матрицами
