Определяем средние значения ( и
и  ) и дисперсии (S2{X} и S2{Y}) для совокупностей:
) и дисперсии (S2{X} и S2{Y}) для совокупностей:

| (3.1) |

| (3.2) |
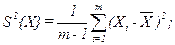
| (3.3) |

| (3.4) |
Расчет коэффициентов парной корреляции
И определение их значимости
Значение коэффициентов парной корреляции рассчитываем по формуле

| (3.5) |
По значению коэффициентов парной корреляции можно сделать определенные выводы о тесноте корреляционной взаимосвязи между случайными величиными X и Y.
Для определения значимости коэффициента корреляции определяем расчётное значение критерия Стьюдента:

| (3.6) |
Теоретическое значение критерия tT определяем по таблице приложения Д при условии, что РD = 0,95 и f = m – 2. Если tR {rYX} > tТ, то гипотеза о наличии корреляционной взаимосвязи между X и Y не отвергается.
Определение линейной модели корреляционной взаимосвязи
Рассчитываем значения коэффициентов линейных уравнений сопряженных прямых:
 ; ; 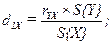 
| (3.7) |
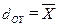 ; ; 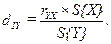
| (3.8) |
Подставляем полученные значения в соответствующие уравнения:


| (3.9) |
Раскрываем скобки и получаем уравнения прямых. Строим оси координат, наносим корреляционное поле точек, а затем строим сопряженные прямые с углом φ между ними.

Рисунок 3.1 – Линейные модели корреляционной взаимосвязи
ТРЕБОВАНИЯ К ОТЧЕТУ
Отчет о выполнении лабораторной работы должен содержать:
¾ тему и цель лабораторной работы;
¾ необходимые теоретические сведения по теме;
¾ исходную совокупность случайных величин (по заданию преподавателя);
¾ поэтапное определение коэффициента корреляции и линейной модели корреляционной взаимосвязи;
¾ выводы по результатам определения статических корреляционных однофакторных моделей по данным пассивного эксперимента;
¾ график сопряженных прямых;
¾ отметку преподавателя о выполнении лабораторной работы.
Лабораторная работа № 4
ОПРЕДЕЛЕНИЕ СТАТИЧЕСКИХ КОРРЕЛЯЦИОННЫХ
МНОГОФАКТОРНЫХ МОДЕЛЕЙ ПО ДАННЫМ
ПАССИВНОГО ЭКСПЕРИМЕНТА
Цель работы: расчет парных коэффициентов корреляции, множественного коэффициента корреляции, определение его значимости и линейной модели корреляционной взаимосвязи.
ОСНОВНЫЕ СВЕДЕНИЯ
В том случае, если требуется проанализировать зависимость одной случайной величины (Y) от нескольких случайных величин Х1, Х2,..., ХМ, необходимо определить корреляционную многофакторную модель:
Y = a0 + a1X1 + a2X2 +... + aMXM.
Методику рассмотрим на примере разработки двухфакторной корреляционной модели. В результате дискретных измерений факторов X1, Х2 и выходного параметра Y получают совокупность сопряженных случайных чисел (можно воспользоваться совокупностями, приведенными в приложении А).






