В тех случаях, когда выборка имеет большой объем, т.е. число значений более 30, для упрощения расчетов применяют «способ отсчета от условного нуля». Полученный ряд экспериментальных значений делят на классы (интервалы). Исходя из количества элементов совокупности m, число классов k определяют по формуле (с округлением до целого):
k = 3,332·lg (m +1) при 50 < m < 200;
k =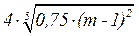 
при m > 200.
Например, для m = 50 принимаем k = 7.
Находим в анализируемой выборке максимальное Ymax и минимальное Ymin значения и определяем величину интервала:
 .
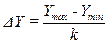| (2.1) |
Составляем таблицу и разносим все значения анализируемой совокупности по соответствующим классам.
| № класса | К | k | |||
| Границы класса |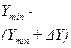 
| 
| 
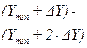
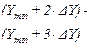
| К |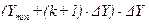 
|
| Значения Yi | |||||
| Частота mi | |||||
| Среднее Yi* |
Количество случайных величин в каждом классе mi называется частотой. После сортировки значений определяем частоту mi и математическое ожидание (среднее) Yi* в каждом классе.
Дальнейшие расчеты сводим в таблицу.
| Границы классов | mi | Yi* | yi | mi·yi | yi2 | mi·yi2 | miT |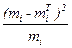 
| |
| -3 | |||||||||
| -2 | |||||||||
| -1 | |||||||||
| Σ | ¾ | ¾ | ¾ | ¾ | ¾ |
Значение Yi* в том классе, где mi принимает максимальное значение, называется условным нулем выборки Y0*.
Значения yi находятся по формуле (и округляются до ближайшего целого):
 .
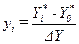| (2.2) |
Определение оценок математического ожидания,
Среднего квадратического отклонения и квадратической неровноты
По способу отсчета от условного нуля находим среднее значение выборки:
 .
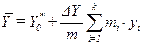| (2.3) |
Находим среднее квадратическое отклонение и квадратическую неровноту:
 ;
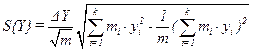| (2.4) |
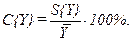
| (2.5) |
Определение закона распределения исследуемой величины
Задаемся видом предполагаемой дифференциальной или интегральной функции распределения. Как правило, случайные величины, являющихся предметом анализа при исследовании технологических процессов легкой промышленности, отвечают нормальному закону распределения:
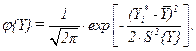
| (2.6) |
Вычисляем теоретические частоты miT в каждом классе:
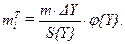
| (2.7) |
Полученные значения заносим в таблицу и определяем наблюдаемое значение критерия Пирсона:
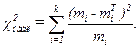
| (2.8) |
По таблице приложения Г определяем критическое значение критерия Пирсона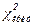 
при условии, что доверительная вероятность PD = 0,95 и число степеней свободы f = k − 2.
Если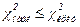 
, то анализируемую величину можно считать распределенной по нормальному закону. Если 
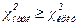, необходимо использовать другие функции (логнормальную, экспоненциальную, показательно-степенную и др.) до нахождения распределения, адекватного исследуемой случайной величине.
