Таблица 2.1. Используемые обозначения
| Обозначение | Наименование |
a, b, c, 
| Вектор |
|
| a |, ||
| Модуль вектора |
| ax, ay, az | Координаты вектора в декартовых координатах |
| r 1 = (x 1, y 1, z 1), r 2 = (x 2, y 2, z 2) | Радиус-векторы точек с координатами (x 1, y 1, z 1), (x 2, y 2, z 2) |
| a · b, ab | Скалярное произведение |
| a 2 | Скалярный квадрат |
| пр b a | Проекция вектора a на вектор b |
| a ´ b | Векторное произведение |
| ^ | Знак ортогональности двух векторов |
| || | Знак коллинеарности двух векторов |
| Ð | Знак угла |
| abc, (abc) | Смешанное произведение трех векторов |
Таблица 2.2. Геометрический вектор
| Наименование | Обозначение, формула | |
| Вектор и его выражение в декартовых координатах | a = ax i + ay j + az k = (ax, ay, az) | |
| Модуль вектора | 
| |
| Направляющие косинусы вектора и их свойство |  ;
cos2a + cos2b + cos2g = 1
| |
| Сложение двух векторов | a + b = (ax + bx, ay + by, az + bz) | |
| Умножение вектора на скаляр | l a = (l ax, l ay, l az) | |
| Вектор с началом в точке A (x 1, y 1, z 1) и с концом в точке
B (x 2, y 2, z 2)
|
= (x 2- x 1) i + (y 2- y 1) j + (z 2- z 1) k
| |
| Длина отрезка AB, заданного граничными точками A (x 1, y 1, z 1) и B (x 2, y 2, z 2) | l = | r 2- r 1 |;
l = 
| |
| Условие коллинеарности двух векторов a и b (a || b) | l a = b или 
| |
| Проекция вектора a на вектор b | пр b a = | a | cos j, j =Ð(a, b) | |
| Деление отрезка AB в данном отношении l = AC / CB, где A (x 1, y 1, z 1), B (x 2, y 2, z 2), С (x, y, z) Частный случай: деление отрезка пополам |
| |
| Длины диагоналей параллелограмма, построенного на векторах a и b | d 1,2 = | a ± b |;
d 1,2 = 
| |
Таблица 2.3. Скалярное произведение
| Наименование | Обозначение, формула | ||||
| Определение скалярного произведения двух векторов | ab = | a |×| b | cosj, j =Ð(a, b) | ||||
| Таблица скалярного умножения в декартовых координатах | × | i | j | k | |
| i | |||||
| j | |||||
| k | |||||
| Скалярное произведение в декартовых координатах | ab = axbx + ayby+ azbz | ||||
| Скалярный квадрат | a 2 = | a |2 = 
| ||||
| Свойства: 1) переместительное 2) сочетательное относительно скалярного множителя 3) распределительное | ab = ba l(ab) = (l a) b = a (l b) a (b + c) = ab + ac | ||||
| Условие ортогональности двух ненулевых векторов | ab = 0  a ^ b
| ||||
| Условие ортогональности в декартовых координатах | axbx + ayby+ azbz = 0 | ||||
| Приложения: 1) Угол между двумя векторами 2) Проекция вектора a на вектор b | cosj =  =
пр b a = 
|
Таблица 2.4. Векторное произведение
| Наименование | Обозначение, формула | ||||
| Определение векторного произведения двух векторов | a ´ b = c, | c | = | a |×| b | sin j, j =Ð(a, b), c ^ a, c ^ b (a, b, c) - правая тройка векторов | ||||
| Таблица векторного умножения в декартовых координатах | ´ | i | j | k | |
| i | o | k | - j | ||
| j | - k | o | i | ||
| k | j | - i | o | ||
| Векторное произведение в декартовых координатах | 
| ||||
| Свойства: 1) антипереместительное 2) сочетательное относительно скалярного множителя 3) распределительное | a ´ b = - b ´ a l(a ´ b) = (l a)´ b = a ´(l b) a ´(b + c) = a ´ b + a ´ c | ||||
| Условие коллинеарности двух ненулевых векторов |
 a||b
| ||||
| Условие коллинеарности в декартовых координатах | 
| ||||
| Приложения: 1) Площадь параллелограмма, построенного на векторах a и b как на сторонах 2) Площадь треугольника, две стороны которого образованы данными векторами a и b |
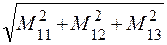
| a ´ b | = 
 | a ´ b | =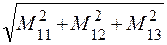
|
Обозначения:
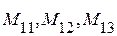- миноры элементов i, j, k соответственно в определителе для
векторного произведения в декартовых координатах
Таблица 2.5. Смешанное произведение
| Наименование | Обозначение, формула |
| Определение и обозначение смешанного произведения трех векторов | (a ´ b)× c = abc |
| Смешанное произведение в декартовых координатах | 
|
| Свойства: 1) изменение знака при перестановке двух сомножителей 2) не изменяется при циклической перестановке сомножителей 3) векторы a, b, c образуют в порядке следования а) правую тройку векторов, если б) левую тройку векторов, если | abc = - acb = - cba = - bac abc = bca = cab abc > 0 abc < 0 |
| Условие компланарности трех ненулевых векторов | abc =0 a, b, c - компланарны
|
| Условие компланарности в декартовых координатах | 
|
| Приложения: 1) Объем параллелепипеда, построенного на векторах a, b, c как на ребрах 2) Объем треугольной призмы, построенной на векторах a, b, c как на ребрах 3) Объем тетраэдра, построенного на векторах как на ребрах a, b, c | | abc |
| abc |
 | abc |
|
