14.8. Составить уравнение плоскости, проходящей через точку
M (2; – 3; 0) и прямую 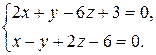
14.9. Найти величину острого угла между прямой
 и плоскостью 2 x + y + 2 z – 5 = 0.
и плоскостью 2 x + y + 2 z – 5 = 0.
14.10. Написать уравнение плоскости, проходящей через параллельные прямые 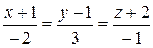 и
и 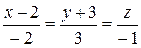 .
.
14.11. Найти координаты точки пересечения прямой
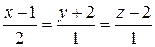 с плоскостью 3 x – y + 2 z + 5 = 0.
с плоскостью 3 x – y + 2 z + 5 = 0.
14.12. При каком значении m прямая  параллельна плоскости 5 x – 3 y + 4 z – 1 = 0?
параллельна плоскости 5 x – 3 y + 4 z – 1 = 0?
14.13. При каких значениях C и D прямая 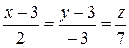 лежит в плоскости 2 x – y + Cz + D = 0?
лежит в плоскости 2 x – y + Cz + D = 0?
Ответы к занятию 14
14.1. q = (– 3, 4, 5). 14.2. a) 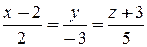 ; б)
; б) 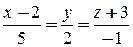 ;
;
в) 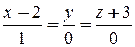 ; г)
; г) 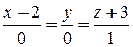 ; д)
; д)  ;
;
е)  . 14.3.
. 14.3. 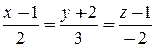 .
.
14.4. а) x – 2 y + z = 0; б) 2 x + y – 1 = 0. 14.5. q = (1, 7, 5).
14.6. 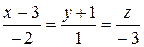 . 14.7. а) 1/
. 14.7. а) 1/ 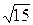 , (1, – 6, – 4); б) 3 x – y + 2 z – 1 = 0.
, (1, – 6, – 4); б) 3 x – y + 2 z – 1 = 0.
14.8. 6 x – 3 y + 2 z – 21 = 0. 14.9. p/4. 4.10. 2 x + y – z – 1 = 0.
14.11. (– 3; – 4; 0). 14.12. 6. 14.13. C = – 1; D = – 3.
Занятие 15. Кривые второго порядка
Изучаемый материал: понятие кривой второго порядка; канонические уравнения окружности, эллипса, гиперболы и параболы; элементы симметрии, вершины, фокусы, фокальные свойства; параметры и связь между параметрами кривых второго порядка.
| 1. Окружность | 15.1 | 15.9 | 15.17 - 15.20 |
| 2. Эллипс | 15.2, 15.3 | 15.10, 15.11 | 15.21, 15.22 |
| 3. Гипербола | 15.4, 15.5 | 15.12, 15.13 | 15.23, 15.24 |
| 4. Парабола | 15.6 - 15.8 | 15.14 - 15.16 | 15.25, 15.26 |
15.1. Установить, что каждое из следующих уравнений определяет окружность, найти ее центр C и радиус R:
a) x 2 + y 2 – 4 x + 6 y – 3 = 0; б) x 2 + y 2 – 8 x = 0.
15.2. Построить эллипс 9 x 2 + 25 y 2 = 225. Найти: a) полуоси;
б) координаты фокусов; в) эксцентриситет.
15.3. Составить каноническое уравнение эллипса, проходящего через точки M 1(2; – 4  ) и M 2(– 1; 2
) и M 2(– 1; 2 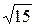 ).
).
15.4. Построить гиперболу 16 x 2 – 9 y 2 = 144. Найти: a) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения асимптот.
15.5. Дан эллипс 5 x 2 + 8 y 2 = 40. Найти уравнение гиперболы, вершины которой находятся в фокусах, а фокусы – в вершинах данного эллипса.
15.6. Построить следующие параболы и найти их параметры:
a) y 2 = 6 x; б) x 2 = – y.
15.7. Парабола симметрична относительно оси Ox, ее вершина находится в начале координат. Составить каноническое уравнение параболы, зная, что она проходит через точку A (– 3; – 3).
15.8. Через фокус параболы y 2 = 12 x проведена хорда, перпендикулярная к ее оси. Найти длину хорды.






