Таблица 4.1. Канонические уравнения кривых второго порядка
| Окружность | |||||||||
| каноническое уравнение | уравнение с центром в точке (x o, y o) | параметрические уравнения | |||||||
| x 2 + y 2 = R 2 | (x - x o)2 + (y - y o)2 = R 2 | 
| |||||||
| R - радиус окружности | |||||||||
| Эллипс | |||||||||
| каноническое уравнение | уравнение с центром в точке (x o, y o) | параметрические уравнения | |||||||
| 
| 
| |||||||
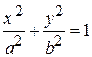
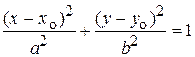
| Параметры: a, b - полуоси (a > b) a - большая полуось b – малая полуось | c - фокусное расстояние e - эксцентриситет t – параметр | Основные соотношения:
c 2 = a 2 - b 2;
e =  ; 0 £ e < 1
| |||||||
| Гипербола | |||||||||
| каноническое уравнение: | уравнение с центром в точке (x o, y o): | параметрические уравнения: | уравнения асимптот: | ||||||
| 
| 
| 
| ||||||
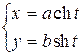
| Параметры: a, b - полуоси a - действительная полуось b - мнимая полуось | c – фокусное расстояние e – эксцентриситет t – переменный параметр | Основные соотношения: c 2 = a 2 + b 2;
e = ; e > 1
| |||||||
| Парабола | |||||||||
| каноническое уравнение: y 2 = 2 px | Уравнение с вершиной в точке (x o, y o): (y - y o)2 = 2 p (x - x o) | уравнение директрисы: x = p /2 | |||||||
| p – параметр | |||||||||
Таблица 4.2. Свойства кривых второго порядка
| Наименование | Эллипс | Гипербола | Парабола |
Чертеж:
M – текущая
точка,
 r, r 1, r 2 -
фокальные
радиусы
|   Y
| y  
| y   
|
| Координаты фокусов | F 1(– c, 0), F 2(+ c, 0) | F 1(– c, 0), F 2(+ c, 0) | F (p/ 2, 0) |
| Каноническое уравнение |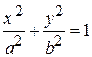
|
| y 2 = 2 px |
| Элементы симметрии | Две оси симметрии и центр симметрии | Две оси симметрии и центр симметрии | Одна ось симметрии |
| Вершины | Четыре вершины | Две вершины | Одна вершина |
| Фокальные радиусы | r 1 = a + ex r 2 = a - ex | r 1 = ex + a r 2 = ex - a |
r =  + x
|
| Фокальное свойство | r 1 + r 2 = 2 a | | r 1 - r 2| = 2 a | r = d |
| Директриса | x = - p/ 2 | ||
| Оптическое свойство | Световые лучи, исходящие из одного фокуса, после отражения от эллиптического зеркала концентрируются в другом фокусе. | Световые лучи, исходящие из одного фокуса, после отражения от гиперболического зеркала кажутся исходящими из другого фокуса. | Световые лучи, исходящие из фокуса, после отражения от параболического зеркала образуют пучок, параллельный оси симметрии. |
Таблица 4.3. Преобразование декартовой прямоугольной
системы координат на плоскости
Поворот осей координат относительно начала координат:
Обозначения:
j - угол поворота
(x, y) - координаты точки в исходной системе координат
(x¢, y¢) - координаты точки в повернутой системе координат
r =  - радиус-вектор точки в исходной системе координат
r¢ =  - радиус-вектор точки в повернутой системе координат
Матрица поворота:
T j =  ,  = T - j = 
Зависимость между координатами в матричной форме:
r = T j r¢, r¢ = T - j r
и с помощью системы уравнений:
 ; 
|
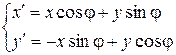
Параллельный перенос осей координат:
Обозначения:
(x o, y o) - координаты начала координат перенесенной системы в исходной
(x¢, y¢) - координаты точки в исходной системе координат
(x², y²) - координаты точки в перенесенной системе
r o =  - радиус-вектор начала координат перенесенной системы в исходной
r¢ = - радиус-вектор точки в исходной системе
r² =  - радиус-вектор точки в перенесенной (новой) системе координат
Зависимость между координатами точки в исходной системе и перенесенной (новой) системе
в матричной форме: r¢ = r² + r o, r² = r¢ - r o
и с помощью системы уравнений:  , 
|
Таблица 4.4. Нахождение матрицы поворота к главным
направлениям квадратичной формы
Исходные данные:
F (x, y) = a 11 x 2 + 2 a 12 xy + a 22 y 2 - квадратичная форма
A =  - матрица квадратичной формы
|
¯
Составление характеристического уравнения и его решение:
| A - l E | = 0 или  = 0;
l1 и l2 - корни характеристического уравнения
|
¯
Подстановка корней характеристического уравнения l1 и l2 в матричное уравнение Ar = l r или в систему уравнений  .
Примечание. Уравнения системы являются линейно зависимыми, поэтому следует использовать одно из них.
|
¯
Вычисление собственных векторов r 1 =  и r 2 =  .
Примечания. 1. При вычислении собственных векторов r 1 и r 2 одна из координат этих векторов задается произвольно.
2. Поскольку векторы r 1 и r 2 ортогональны, то ×условие r 1× r 2 = 0 можно использовать для контроля правильности вычислений.
|
¯
Нормирование собственных векторов: e 1 =  r 1, e 2 =  r 2.
|
¯
| Составление матрицы поворота к главным направлениям квадратичной формы:
T j = || e 1| e 2|| = .
Примечания. 1. Направления векторов e 1 и e 2 рекомендуется выбирать такими, чтобы диагональные элементы матрицы T j были положительными; тогда поворот производится на острый угол.
2. Если sin j > 0, то поворот в положительном направлении (против часовой стрелки); если же sin j < 0, то поворот в отрицательном направлении.
|
¯
| Вычисление угла поворота j по элементам матрицы T j. |
Таблица 4.5. Схема упрощения уравнения кривой второго порядка
| Исходные данные: общее уравнение кривой второго порядка a 11 x 2 + 2 a 12 xy + a 22 y 2 + 2 b 1 x + 2 b 2 y + c = 0, где F (x, y) = a 11 x 2 + 2 a 12 xy + a 22 y 2 - квадратичная форма, L (x, y) = 2 b 1 x + 2 b 2 y - линейная часть, c - свободный член. |
¯
| Получение собственных чисел l1 и l2 и матрицы T j поворота к главным направлениям квадратичной формы F (x, y). |
¯
Поворот осей координат к главным направлениям квадратичной формы (кривой): а) преобразование квадратичной формы к каноническому виду
F (x¢, y¢) = l1 x¢ 2 + l2 y¢ 2;
б) преобразование линейной части L (x¢, y¢) = 2= || b 1 b 2|| T j = 2  x¢ + 2  y¢.
Результат: уравнение кривой в повернутых координатах:
l1 x¢ 2 + l2 y¢ 2 + 2 x¢ + 2 y¢ + c = 0.
|
¯
Параллельный перенос начала координат (системы координат O¢x¢y¢) в точку ( ,  ):
а) если l1×l2 ¹ 0, то (, ) - центр кривой; выделяются полные квадраты для переменных x¢ и y¢.
Результат: l1(x¢ - )2 + l2(y¢ - )2 = с².
б) если l1×l2 = 0, то (, ) - вершина кривой (параболы); выделяется полный квадрат для x¢, если l1 ¹ 0, и для y¢, если l2 ¹ 0.
Результат: l1(x¢ - )2 = -2 (y¢ - ) или l2(y¢ - )2 = -2 (x¢ - ).
|
¯
| Запись полученных уравнений в преобразованных координатах путем замены
x¢ - = x², y¢ - = y²: а) l1 x² + l2 y² = с²;
б) l1 x² 2 = -2 y² или l2 y² 2 = -2 x².
|
¯
| Запись полученных уравнений в каноническом виде: | ||
1. Случай l1×l2 > 0:
кривая эллиптического типа, каноническое уравнение  .
| 2. Случай l1×l2 < 0:
кривая гиперболического типа, каноническое уравнение  .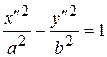
| 2. Случай l1×l2 = 0: кривая параболического типа, каноническое уравнение y² 2 = 2 px² или x² 2 = 2 py². |
¯
| Результат упрощения: каноническое уравнение кривой второго порядка. |
Примечания к табл. 4.5.
1. При упрощении уравнений кривых второго порядка возможны вырожденные и мнимые случаи, которые здесь не рассматриваются.
2. Если в исходном уравнении a 12 = 0, то производится только параллельный перенос системы координат.
Таблица 4.6. Канонические уравнения поверхностей второго порядка
| Цилиндрические поверхности (случай F (x,y) = 0) | |||||
1) эллиптический
цилиндр
|
2) гиперболический
цилиндр
| 3) параболический цилиндр y 2=2 px | |||
| Поверхности, имеющие центр симметрии | |||||
1) эллипсоид
| 2) сфера x 2 + y 2 + z 2 = R 2 |
3) конус
| |||
4) однополостный гиперболоид
|
5) двуполостный гиперболоид
| ||||
| Параболоиды | |||||
1) эллиптическийпараболоид
 , p > 0, q > 0
|
2) гиперболическийпараболоид
 , p > 0, q > 0
| ||||
Примечание. Для каждого вида поверхности приведен один вариант канонического уравнения.
