В задачах 12.5 - 12.7 исследовать взаимное расположение заданных прямых L 1 и L 2. Найти:
1) расстояние r между прямыми, если они параллельны;
2) cosj (j - угол между прямыми) и точку пересечения прямых в противном случае.
12.5. L 1: x + y – 1 = 0, L 2: 2 x – 2 y + 1 = 0.
12.6. L 1: x + y – 1 = 0, L 2: 
.
12.7. L 1: – x + 2 y + 1 = 0, L 2: 2 x – 4 y – 2 = 0.
12.8. Треугольник ABC задан координатами своих вершин:
A (2, – 2), B (6, 1), C (– 2, 0). Требуется:
а) написать уравнение стороны AB;
б) написать уравнение высоты CD и вычислить ее длину hc;
в) найти угол j между высотой CD и медианой BM.
12.9. Показать, что точка (– 1, 2) принадлежит прямой L: x = 2 t, y = – 1 – 6 t. Найти соответствующее этой точке значение параметра t.
12.10. Написать уравнение прямой, проходящей через точку M o (– 2, 3) на одинаковых расстояниях от точек M 1(5, – 1) и M 2(3, 7).
Дополнительное задание 12
12.11. При каких значениях a следующие пары прямых параллельны и перпендикулярны?
а) 2 x – 3 y + 4 = 0 и a x – 6 y + 7 = 0;
б) a x – 4 y + 1 = 0 и – 2 x + y + 2 = 0;
в) 4 x + y – 6 = 0 и 3 x + a y – 2 = 0;
г) x – a y + 5 = 0 и 2 x + 3 y + 3 = 0.
12.12. Найти уравнение прямой, проходящей через точку A (–1; 2):
а) параллельно прямой y = 2 x – 7;
б) перпендикулярно прямой x + 3 y – 2 = 0.
12.13. Через точку пересечения прямых 3 x – 2 y + 5 = 0,
x + 2 y – 9 = 0 проведена прямая, параллельная прямой 2 x + y + 6 = 0. Составить ее уравнение.
12.14. Найти координаты точки M 2, симметричной точке
M 1(– 3; 4) относительно прямой 4 x – y – 1 = 0.
12.15. Найти площадь треугольника, образованного прямыми:
2 x + y + 4 = 0, x + 7 y – 11 = 0 и 3 x – 5 y – 7 = 0.
Ответы к занятию 12
12.1. (– 3/4, – 1/2), cos j = 1/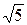 
. 12.2. (1, 0), cosj = 2/ .
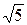12.3. а) AB: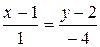 
; б) CD: 
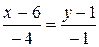, hc = 19/ 
;
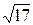в) cosj = 19/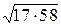 
.
12.5. Перпендикулярны. 12.6. Параллельны, r =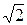 
. 12.7. Совпадают.
12.8. а) AB: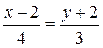 
; б) CD: 
, hc = 4; в) cos j = 1/ 
.
12.9. t = – 1/2. 12.10. x – 4 y + 8 = 0.
12.11. а) 4; – 9; б) 8; – 2; в) 3/4; – 12; г) – 3/2; 2/3.
12.12. а) 2 x – y + 4 = 0; б) 3 x – y + 5 = 0. 12.13. 2 x + y – 6 = 0.
12.14. (5; 2). 12.15. 13.
Занятие 13. Плоскость в пространстве
Изучаемый материал: общее уравнение; неполные уравнения; уравнение плоскости, проходящей через данную точку перпендикулярно данному направлению; уравнение плоскости, проходящей через три заданные точки; уравнение в отрезках; взаимное положение двух плоскостей; угол между двумя плоскостями; условия параллельности и перпендикулярности двух плоскостей.
| 1.Разные задачи | 13.1 - 13.5 | 13.9 - 13.13 | 13.17 - 13.23 |
| 2. Взаимное расположение плоскостей | 13.6, 13.7 | 13.14, 13.15 | |
| 3. Объем пирамиды | 13.8 | 13.16 |
13.1. Заданы плоскость P: – 2 x + y – z + 1 = 0 и точка M (1, 1, 1). Написать уравнение плоскости P', проходящей через точку M параллельно плоскости P, и вычислить расстояние r между плоскостями.
13.2. Написать уравнение плоскости P', проходящей через заданные точки M 1(1, 2, 0) и M 2(2, 1, 1) перпендикулярно заданной плоскости P: – x + y – 1 = 0.
13.3. Написать уравнение плоскости, проходящей через точку M (1, 1, 1) параллельно векторам a = (0, 1, 2) и b = (– 1, 0, 1).
13.4. Написать уравнение плоскости, проходящей через точки A (1, 2, 0) и
B (2, 1, 1) параллельно вектору a = (3, 0, 1).
13.5. Написать уравнение плоскости, проходящей через три заданные точки A (1, 2, 0), B (2, 1, 1) и C (3, 0, 1).
В задачах 13.6 и 13.7 исследовать взаимное расположение плоскостей P 1 и P 2. В случае параллельности плоскостей найти расстояние r между ними, в противном случае - косинус угла между ними.
13.6. P 1: – x + 2 y – z + 1 = 0, P 2: y + 3 z – 1 = 0.
13.7. P 1: 2 x – y + z – 1 = 0, P 2: – 4 x + 2 y – 2 z – 1 = 0.
13.8. Вычислить объем пирамиды, ограниченной плоскостью
P: 2 x – 3 y + 6 z – 12 = 0 и координатными плоскостями.
