10.18. Найти координаты вектора a ´ (2 a + b), если a = (3, – 1, – 2),
b = (1, 2, – 1).
10.19. Даны векторы a = i + 2 j – 3 k, b = – 2 i + j + k.
Найти c = (a – b) ´ (2 b); | c |.
10.20. Найти единичный вектор c, перпендикулярный каждому из векторов
a = (3; – 1; 2) и b = (– 1; 3; – 1).
10.21. Найти единичный вектор e, перпендикулярный вектору
a = (1; 4; 3) и оси абсцисс.
10.22. Вычислить площадь параллелограмма, построенного на векторах
a = (8; 4; 1) и b = (2; – 2; 1).
10.23. Вычислить площадь треугольника с вершинами A (1, – 2, 3),
B (1, 1, 4), C (3, 2, 1).
10.24. Вычислить площадь параллелограмма, построенного на векторах
a = 3 p + 2 q и b = 2 p – q, где | p | = 4, | q | = 3, Ð(p, q) = 3p/4.
10.25. При каком значении l векторы a = (1; 1; l), b = (0; 1; 0) и
c = (3; 0; 1) компланарны?
10.26. Вектор c перпендикулярен векторам a и b; Ð(a, b) = p/6,
| a | = 6, | b | = 3, | c | = 3. Найти abc.
10.27. Вычислить объем тетраэдра с вершинами в точках A (1, 4, 1),
B (– 2, 3, 2), C (4, 6, 2), D (1, 1, 0).
10.28. Объем тетраэдра равен 5, три его вершины находятся в точках
A (2, 1, – 1), B (3, 0, 1), C (2, – 1, 3). Найти координаты четвертой вершины D,
если известно, что она лежит на оси ординат.
Ответы к занятию 10
10.1. 2(k – i). 10.2. 2 a ´ c. 10.3. 50 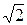 . 10.4. 2
. 10.4. 2  .
.
10.5. – 7; a) левая; б) правая; в) правая. 10.6. Нет. 10.7. 2. 10.8. 3 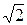 .
.
10.9. a || b. 10.10. a ´ c. 10.11. 3. 10.12. 5. 10.13.  /2. 10.14. 3
/2. 10.14. 3 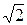 /2.
/2.
10.15. Да. 10.16. 6. 10.18. (5; 1; 7). 10.19. (10; 10; 10), 10  .
.
10.20. ±  (5; – 1; – 8). 10.21. ±(0; 3/5; – 4/5). 10.22. 18
(5; – 1; – 8). 10.21. ±(0; 3/5; – 4/5). 10.22. 18  .
.
10.23. 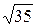 . 10.24. 42
. 10.24. 42 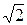 . 10.25. 1/3. 10.26. ±27.
. 10.25. 1/3. 10.26. ±27.
10.27. 2,5. 10.28. (0; 8; 0).
ПосАиГ-П-5-07
Занятие 11. Прямая линия на плоскости
Изучаемый материал: общее уравнение прямой; неполные уравнения; каноническое уравнение; уравнение с угловым коэффициентом; уравнение в отрезках; параметрические уравнения, уравнения прямой, через одну точку и через две точки.
| 1. Разные уравнения прямой | 11.1 – 11.3 | 11.5 - 11.7 | |
| 2. Разные задачи | 11.4 | 11.8 | 11.9 - 11.18 |
В задачах 11.1 – 11.3 написать уравнения прямой во всех возможных формах.
11.1. Прямая L задана точкой M o(– 1, 2) Î L и нормальным вектором
n = (2,2).
11.2. Прямая L задана точкой M o(– 1, 2) Î L и направляющим вектором
q = (3, – 1).
11.3. Прямая L задана двумя своими точками M 1 (1, 2) и M 2 (–1, 0).
11.4. Заданы прямая L: – 2 x + y – 1 = 0 и точка M (– 1, 2). Требуется:
а) вычислить расстояние r от точки M до прямой L;
б) написать общее уравнение прямой L', проходящей через точку M перпендикулярно заданной прямой L;
в) написать общее уравнение прямой L", проходящей через точку M параллельно заданной прямой L;
г) написать общее уравнение прямой, проходящей через точку M, если эта точка является основанием перпендикуляра, опущенного из начала координат на эту прямую;
д) вычислить площадь треугольника, образованного осями координат и прямой L.




