9.9. Дано: | a | = 3, | b | = 4, Ð(a, b) = 2p/3. Вычислить (a + b)2.
9.10. Дано: | a | = 3, | b | = 5. Определить, при каком значении a векторы
(a + a b) и (a – a b) будут ортогональны.
9.11. Вычислить a · b, если a = 3 m + 2 n, b = m – n, где m и n - ортогональные векторы, | m | = 2, | n | = 1.
9.12. Дано: | a | = 3, | b | = | c | = 2. Векторы a и b ортогональны, а вектор c образует с ними углы, равные π/3. Вычислить (2 a – b) · (с – b).
9.13. Даны векторы a = (4, – 2, – 4) и b = (6, – 3, 2). Вычислить:
a) a · b; б) (2 a – 3 b)(a + 2 b); в) (a – b)2; г) |2 a – b |; д) пр a b; е) пр ba;
ж) направляющие косинусы вектора a;. з) пр a + b (a –2 b); и) cos (a, b).
9.14. Доказать, что четырехугольник с вершинами A (– 3, 5, 6), B (1, – 5, 7),
C (8, – 3, – 1), D (4, 7, – 2) является квадратом.
9.15. Найти cos j, где j - угол между диагоналями AC и BD параллелограмма, если заданы три его вершины: A (2, 1, 3), B (5, 2, – 1), C (– 3, 3, – 3).
Дополнительное задание 9
9.16. Дано: | a | = 3, | b | = 4, j =Ð(a, b) = 120°. Найти модуль вектора
c = 3 a + 2 b.
9.17. Единичные векторы e 1, e 2, e 3, удовлетворяют условию
e 1 + e 2 + e 3 = o. Найти e 1· e 2 + e 2 · e 3 + e 3· e 1.
9.18. Вычислить a · b, если a = 3 m + 2 n, b = 2 m + n, где m и n - ортогональные векторы, | m | = 2, | n | = 1.
9.19. Дано: | a | = 3, | b | = | c | = 2. Векторы a и b ортогональны, а вектор c образует с ними углы, равные π/3. Вычислить (2 a + 3 b) · (с – b).
9.20. Найти угол между диагоналями параллелограмма, построенного на векторах a = 2 i + j и b = – j + 2 k..
9.21. При каком значении l векторы b = l i – 5 j + 3 k и
c = i + 2 j – l k взаимно перпендикулярны?
9.22. Какой угол образуют единичные векторы a и b, если известно, что векторы m = a + 2 b и n = 5 a – 4 b взаимно перпендикулярны.
Ответы к занятию 9
9.1. a) 9; б) – 61. 9.2. p/3. 9.3. 1. 9.4. – 5. 9.5. – 5. 9.6. cosj =  .
.
9.7.  . 9.8.
. 9.8. 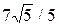 ;
;  . 9.9. 13. 9.10. a =
. 9.9. 13. 9.10. a =  3/5. 9.11. 10. 9.12. 7.
3/5. 9.11. 10. 9.12. 7.
9.13. a) 22; б) – 200; в) 41; г)  ; д) 11/3; е) 22/7;
; д) 11/3; е) 22/7;
ж) cosa = 2/3, cosb = – 1/3, cosg = – 2/3; з) – 84/  ; и) 11/21.
; и) 11/21.
9.15. cosj = 43/25 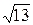 . 9.16.
. 9.16.  . 9.17. – 1,5. 9.18. 26. 9.19. 0.
. 9.17. – 1,5. 9.18. 26. 9.19. 0.
9.20. p/2. 9.21. – 5. 9.22. p/3.
Занятие 10. Векторное и смешанное






