13.17. Составить уравнение плоскости, проходящей через:
а) точку M (– 2, 3, 1) параллельно плоскости Oxy; б) точку M и ось Oy.
13.18. Составить уравнение плоскости, проходящей через:
а) точку A (5, – 4, 6) перпендикулярно оси Ox;
б) точку A и отсекающей равные отрезки на координатных осях.
13.19. Написать уравнение плоскости:
а) параллельной оси Oz и проходящей через точки M 1(3, – 1, 2) и M 2(– 1, 2, 5);
б) проходящей через точку M 1 перпендикулярно вектору 
.
13.20. Найти длину перпендикуляра, опущенного из начала координат на плоскость 20 x – 5 y + 4 z – 210 = 0.
13.21. Найти плоскость, зная, что точка M (2, – 4, 4) служит основанием перпендикуляра, опущенного из начала координат на эту плоскость.
13.22. Составить уравнение плоскости, проходящей через точку M (1, 0, 3) и перпендикулярной к плоскостям x + y + z – 8 = 0 и 2 x – y + 4 z + 5 = 0.
13.23. Составить уравнение плоскости, проходящей через начало координат и точку M (2, 1, – 1) перпендикулярно плоскости 2 x – 3 z = 0.
Ответы к занятию 13
13.1. 2 x – y + z – 2 = 0, 1/ 
. 13.2. x + y – 3 = 0. 13.3. x – 2 y + z = 0.
13.4. – x + 2 y + 3 z – 3 = 0. 13.5. x + y – 3 = 0. 13.6. cosj = 1/2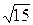 
.
13.7. Параллельны, r = 3/2 . 13.8. 8. 13.9. x – y = 0, 1/ 
.
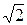13.10 x + 2 y – 2 = 0. 13.11. – x + y + 2 z – 5 = 0. 13.12. 2 x – 2 y – z + 1 = 0.
13.13. 2 x – y – 1 = 0. 13.14. cosj = 1/2. 13.15. Плоскости совпадают.
13.16. 37,5. 3.17. а) z – 1 = 0; б) x + 2 z = 0.
13.18. а) x – 5 = 0; б) x + y + z – 7 = 0.
13.19. а) 3 x + 4 y – 5 = 0; б) – 4 x + 3 y + 3 z + 9 = 0. 13.20. 10.
13.21. x – 2 y + 2 z – 18 = 0. 13.22. 5 x – 2 y – 3 z + 4 = 0. 13.23. 3 x – 4 y + 2 z = 0.
Занятие 14. Прямая и плоскость в пространстве
Изучаемый материал: канонические, параметрические и общие уравнения прямой в пространстве; уравнения прямой, проходящей через две точки; взаимное положение двух прямых; угол между двумя прямыми; условия параллельности и ортогональности двух прямых; взаимное положение прямой и плоскости; угол между ними; нахождение точки пересечения; условия параллельности и перпендикулярности прямой и плоскости.
| 1.Прямая в пространстве | 14.1 - 14.3 | 14.5, 14.6 | |
| 2. Прямая и плоскость | 14.4 | 14.7 | 14.8 - 14.13 |
| 14.1.Прямая L задана общими уравнениями | L: 
|
Написать для нее канонические уравнения.
14.2. Написать канонические уравнения прямой, проходящей через точку
M o(2, 0, – 3) параллельно:
a) вектору q = (2, –3, 5); б) прямой 
; в) оси x; г) оси z;
д) прямой 
; е) прямой x = –2+ t, y = 2 t, z = 1– 
t.
14.3. Написать уравнения прямой, проходящей через две заданные точки
A (1, – 2, 1) и B (3, 1, – 1).
14.4. Даны прямая L: 
и точка M (0, 1, 2) Ï L (проверить!).
Требуется:
а) написать уравнение плоскости, проходящей через прямую L и точку M;
б) написать уравнение плоскости, проходящей через точку M перпендикулярно прямой L.
