8.19. Вектор a составляет с осями Ox и Oy углы a = 60° и b = 120°. Найти его координаты, если | a | = 2.
8.20. При каких значениях a и b векторы a = – 2 i + 3 j + a k и
b =b i – 6 j + 2 k коллинеарны?
8.21. Найти направляющие косинусы вектора a = (14, 2, – 5).
8.22. Являются ли линейно зависимыми следующие системы векторов:
а) (10, 25) и (2, 5); б) (1, 2, 3) и (4, 5, 6); в) (3, 2), (6, 5) и (12, 12);
г) (5, 2, 1), (– 1, 3, 3) и (9, 7, 5).
8.23. Представить вектор d = (4; 12; – 3) как линейную комбинацию векторов a = (2; 3; 1), b = (5; 7; 0) и c = (3; – 2; 4).
8.24. Даны три вектора a = (2, – 1), b = (1, 2), c = (4, 3). Найти разложение вектора m = a + b + c по векторам a и c.
8.25. Луч образует с двумя осями координат углы в 60°. Под каким углом наклонен он к третьей оси?
8.26. На оси Ox найти точку M, расстояние которой от точки A (3, – 3) равно 5.
8.27. Даны вершины треугольника A (3, 1, 5) и векторы 
= (1, – 1, 2),
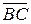= (2, 2, 3), совпадающие с его сторонами. Найти остальные вершины и длину стороны AC.
Ответы к занятию 8
8.1. а) | a | =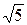 
, a 0 = (– 1/ 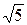, 2/ 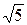, 0); б) 2/ 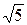; в) – 19/3; г) 0.
8.2. x = – 5 i + 10 j + 10 k. 8.3. (14/27, 22/27, 7/27). 8.4. а) линейно зависимы;
б) линейно независимы; в) линейно зависимы; г) линейно зависимы.
8.5. 2 a + 3 b. 8.6. d = – 2 a + b – c. 8.7. C (6, – 2), D (2, – 4).
8.8. 7. 8.9. (–1, 2, 4) и (8, – 4, – 2).
8.10. a) (2/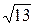 
, 3/ 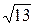, 0); б) (3, 11/2, 0); в) – 2 j; г) 6. 8.11. x = 2 i + 2 j + 2 k.
8.12. (13/23, – 6/23, 18/23). 8.13. а) линейно независимы; б) линейно зависимы; в) линейно зависимы; г) линейно независимы. 8.14. – b + 2 c.
8.15. c =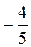 
a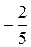 
b. 8.16. D (9, – 5, 6). 8.17. M (0, 1, 0). 8.18. (4, 0) и (5, 2). 8.19. (1, – 1, ± 
). 8.20. a = – 1, b = 4. 8.21. (14/15, 2/15, – 5/15).
8.22. а) линейно зависимы; б) линейно независимы; в) линейно зависимы;
г) линейно зависимы. 8.23. d = a + b – c. 8.24. 
a +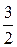 
c. 8.25. 45°.
8.26. (7, 0) и (– 1, 0). 8.27. B (4, 0, 7), C (6, 2, 10), AC =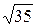 
.
Занятие 9. Скалярное произведение двух векторов
Изучаемый материал: определение скалярного произведения, его физический смысл и свойства; выражение в декартовых координатах; условие ортогональности двух векторов; скалярный квадрат; угол между двумя векторами.
| 1. Скалярное произведение в произвольном базисе | 9.1 - 9.4 | 9.9 - 9.12 | 9.16 - 9.19 |
| 2. Скалярное произведение в декартовых координатах | 9.5 - 9.8 | 9.13 - 9.15 | 9.20 - 9.22 |
9.1. Дано: | a | = 3, | b | = 4, Ð(a, b) = 2p/3. Вычислить: a) a 2; б) (3 a – 2 b)(a + 2 b).
9.2. Найти угол, образованный единичными векторами e 1 и e 2, если известно, что векторы a = e 1 + 2 e 2 и b = 5 e 1 – 4 e 2 ортогональны.
9.3. Вычислить a · b, если a = 2 m – n, b = 2 m + 3 n, где m и n - единичные ортогональные векторы.
9.4. Дано: | a | = 3, | b | = | c | = 2, векторы a и b ортогональны, а вектор c образует с ними углы, равные π/3. Вычислить (3 a + b) · (2 а – c).
9.5. Вычислить скалярное произведение векторов: a = 2 i – 3 j + k и b = – i + j.
9.6. Найти внутренний угол при вершине A треугольника ABC, если
A (– 1, 2), B (1, 1), C (3, 2).
9.7. Треугольник имеет вершины A (4, 2, 2), B (1, – 1, 0), C (3, 2, 4). Найти проекцию стороны AB на сторону AC.
9.8. Даны векторы a = – 2 i + k, b = i + j + 3 k, c = 4 i – j + 5 k.
Найти пр a (b – 2 c), пр b+ca.
