7.17. В треугольнике ABC дано: 
= a, 
= b, точка M - середина стороны BC. Выразить вектор 
через векторы a и b.
7.18. При каких значениях l векторы 2l a и (l3 - 1) a, (a ¹ o), имеют одинаковое направление?
7.19. При каких значениях x векторы x 3 a и (x 2 - x - 2) a, a ¹ o, противоположно направлены?
7.20. Дано: | a | = 13, | b | = 19, | a + b | = 24. Найти: | a - b |.
7.21. Дано: a ^ b, | a | = 5, | b | = 12. Найти: | a + b | и| a - b |.
7.22. В треугольнике ABC: M - точка пересечения медиан треугольника, = a, = b. Разложить и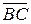 
по векторам a и b.
7.23. В параллелограмме ABCD: K и M - середины сторон BC и CD, 
= a, = b. Выразить векторы 
и 
через a и b.
7.24. Проверить, будут ли линейно зависимы векторы l, m, n, разложенные по трем некомпланарным векторам a, b, c: l = a + 2 b, m = b +2 c, n = c. В случае утвердительного ответа указать связывающую их линейную зависимость.
Ответы к занятию 7
7.2.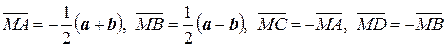 
.
7.3. 
.
7.4. = 
, = 
, 
= 
, 
= 
.
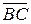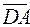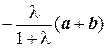7.5. а) -2; б) - 1; в) ± 1. 7.6. а) да, можно; б) c =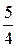 
m + 
n.
7.7. Линейно зависимы, 0 l - 2 m + n = 0.
7.13. а) Линейно независимы; б) линейно независимы; в) линейно зависимы.
7.14. Линейно зависимы; l + m - n = 0. 7.16. l = m = 1. 7.17. 
.
7.18. (- ¥; 0)È(1; ¥). 7.19. (- ¥; - 1)È(0; 2). 7.20. 22. 7.21. 13; 13.
7.22. 3 a - b; 2 b - 3 a. 7.23. 2 b - 2 a. 7.24. Линейно независимы.
Занятие 8. ВЕКТОР В ДекартовЫХ КООРДИНАТАХ
Изучаемый материал: понятие базиса пространства; декартова прямоугольная система координат на плоскости и в пространстве; направляющие косинусы вектора; деление отрезка в данном отношении.
| 1. Операции с векторами | 8.1 - 8.3 | 8.10 - 8.12 | 8.19 - 8.21 |
| 2. Линейная зависимость. Разложение по базису | 8.4 - 8.6 | 8.13 - 8.15 | 8.22 - 8.24 |
| 3. Геометрические задачи | 8.7 | 8.16 | 8.25 - 8.27 |
| 4. Деление отрезка в данном отношении | 8.8, 8.9 | 8.17, 8.18 |
Примечание. Для единичного вектора используется обозначение a 0.
8.1. Заданы векторы a = (– 1, 2, 0), b = (3, 1, 1), c = (2, 0, 1) и d = a – 2 b + 
c.
Вычислить: a) | a | и координаты единичного вектора a 0 вектора a; б)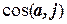 
;
в) координату dx вектора d; г) пр j d.
8.2. Найти вектор x, коллинеарный вектору a = i – 2 j – 2 k, образующий с ортом j острый угол и имеющий длину | x | = 15.
8.3. Найти направляющие косинусы вектора a = (14, 22, 7).
8.4. Являются ли линейно зависимыми следующие системы векторов:
а) (1, 4) и (2, 8); б) (2, – 2, 3) и (4, – 4, 4); в) (3, 2), (6, 4) и (– 12, – 8);
г) (4, 1, 2), (2, 1, 1) и (– 2, 3, – 1).
8.5. Даны три вектора a = (2, – 1), b = (1, 2), c = (4, 3). Найти разложение вектора m = a + b + c по векторам a и b.
8.6. Показать, что тройка векторов a = (1, 0, 0), b = (1, 1, 0), c = (1, 1, 1) образует базис в множестве всех векторов пространства. Вычислить координаты вектора d = –2 i – k в базисе (a, b, c) и написать соответствующее разложение по базису.
8.7. Даны две смежные вершины параллелограмма A (– 2, 6), B (2, 8) и точка
пересечения его диагоналей M (2, 2). Найти две другие вершины.
8.8. Даны вершины треугольника A (3, –1, 5), B (4, 2, –5), C (– 4, 0, 3). Найти длину медианы, проведенной из вершины A.
8.9. Определить координаты концов отрезка, который точками
C (2, 0, 2) и D (5, – 2, 0) разделен на три равные части.
Домашнее задание 8
8.10. Заданы векторы a = 2 i + 3 j, b = – 3 j – 2 k, c = i + j – k. Найти:
a) координаты единичного вектора 
;
б) координаты вектора a – 0,5 b + c;
в) разложение вектора a + b – 2 c по базису (i, j, k);
г) пр j (a – b).
8.11. Найти вектор x, образующий со всеми тремя базисными ортами равные острые углы, если | x | = 2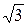 
.
8.12. Найти направляющие косинусы вектора a = (13, – 6, 18)..
8.13. Являются ли линейно зависимыми следующие системы векторов:
а) (1, 4) и (2, 5); б) (2, – 2, 3) и (6, – 6, 9); в) (3, 2), (6, 4) и (– 12, 8);
г) (5, 2, 1), (– 1, 2, 3) и (1, – 1, 3).
8.14. Даны три вектора a = (2, – 1), b = (1, 2), c = (4, 3). Найти разложение вектора m = a + b + c по векторам b и c.
8.15. На плоскости заданы векторы a = (– 1, 2), b = (2, 1) и c = (0, – 2). Убедиться, что (a, b) - базис в множестве всех векторов на плоскости. Построить заданные векторы и найти разложение вектора c по базису (a, b).
8.16. Даны три вершины A (3, – 4, 7), B (– 5, 3, – 2), C (1, 2, – 3) параллелограмма ABCD. Найти его четвертую вершину D, противоположную вершине B.
8.17. На оси ординат найти точку M, равноудаленную от точек A (1, – 4, 7) и
B (5, 6, – 5).
8.18. Отрезок с концами в точках A (3, – 2) и B (6, 4) разделен на три равные части. Найти координаты точек деления.
