Исследовать систему и в случае совместности найти решение:
6.7. 6.8.
. 
.
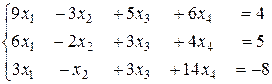Исследовать однородную систему и в случае существования ненулевого решения найти его:
6.9. 
. 6.10. 
.
| 6.11. При каких значениях параметра a однородная система имеет ненулевое решение? | 
|
Дополнительное задание 6
В задачах 6.12 – 6.18 исследовать систему и в случае совместности решить ее.
6.12. 
. 6.13. 
. 6.14. 
.
6.15. 
. 6.16. 
. 6.17.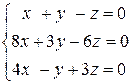 
.
6.18.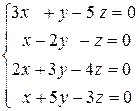 
.
При каких значениях параметра λсистема имеет ненулевое решение?
6.19. 
. 6.20. 
.
Ответы к занятию 6
6.1. (-1; 2; -1).
6.2. Совмест. и неопределенная; 
; 
. 6.3. Несовместная. 6.4. Имеет ненулевое решение; 
.
6.5. Имеет только нулевое решение. 6.6. a 1 = 2, a 2 = - 4.
6.7. Совместная и неопределенная;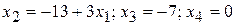 
.
6.8. Несовместная. 6.9. Имеет ненулевое решение; 
.
6.10. Имеет ненулевое решение;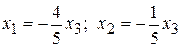 
. 6.11. a = -1.
6.12. Несовместная. 6.13. Совместная и определенная; (2; 3; 5).
6.14. Совместная и неопределенная;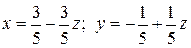 
.
6.15. Несовместная.
6.16. Совмест. и неопределенная (имеет ненулевое решение);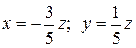 
. 6.17. Совместная и определенная (только нулевое решение).
6.18. Совмест. и неопределенная (имеет ненулевое решение); 
.
6.19. λ1 = - 3, λ2 = 8. 6.20. λ1 = 0, λ2 = 1, λ3 = 2.
ПосАиГ-П-4-07
Занятие 7. Геометрический вектор
Изучаемый материал: понятие геометрического вектора; модуль вектора; коллинеарность и компланарность векторов; линейные операции над векторами; единичный вектор, линейная комбинация векторов, линейно зависимые и линейно независимые векторы.
| 1. Операции с векторами | 7.1- 7.4 | 7.9 - 7.12 | 7.17 - 7.21 |
| 2. Линейно зависимые и линейно независимые векторы | 7.5 - 7.8 | 7.13 - 7.16 | 7.22 - 7.24 |
7.1. Даны векторы a и b. Построить векторы: 3 a, 
b, a +2 b, a – b.
7.2. В параллелограмме ABCD обозначены: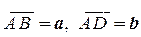 
. Выразить через a и b векторы 
, где M - точка пересечения диагоналей параллелограмма.
7.3. ABCDEF - правильный шестиугольник, причем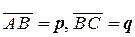 
.
Выразить через p и q векторы 
.
7.4. В трапеции ABCD отношение длины основания AD к длине основания BC равно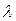 
. Полагая 
и 
, выразить через a и b векторы
.
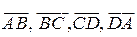7.5. Даны два линейно независимых вектора a и b. При каком значении a следующие пары векторов линейно зависимы (коллинеарны):
а) a a + 2 b и a - b; б) (a+1) a + b и 2 b; в) a a + b и a + a b.
7.6. Даны два линейно независимых вектора m и n. Составлены три вектора:
a = m + 3 n, b = m - n, c = 3 m + 2 n. а) Можно ли векторы a и b принять в качестве базиса двумерного пространства? б) Если да, то разложить вектор c по базису (a, b).
7.7. Проверить, будут ли линейно зависимых векторы l, m, n, разложенные по трем некомпланарным векторам a, b, c. В случае утвердительного ответа указать связывающую их линейную зависимость: l = a - b - c, m = 2 a + b + c,
n = 4 a + 2 b + 2 c.
7.8. Доказать, что для любых заданных векторов a, b и c векторы a + b, b + c и c - a компланарны.
