Домашнее задание 4

Решить системы по правилу Крамера:
4.6. .	4.7. .	4.8. .

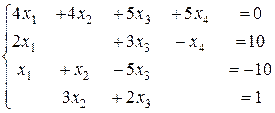Решить матричные уравнения:

4.9. . 4.10. .

4.11. Решить систему уравнений с помощью обратной матрицы:

Дополнительное задание 4

Решить систему по правилу Крамера:

4.12. 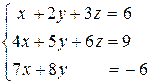. 4.13. 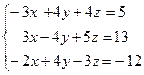. 4.14. .

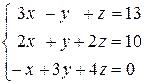Решить матричное уравнение:	4.15. . 4.16. .

4.17. Решить матричное уравнение и сделать проверку:

а) AX = B; ) XA = B, где A = , B = .

Решить матричное уравнение:	4.18. . 4.19. .
4.20.Решить систему уравнений с помощью обратной матрицы:	.

Ответы к занятию 4

4.1. (2; 3). 4.2. (1; 3; 5). 4.3. . 4.4. . 4.5. (2; 3; - 1).

4.6. (2; –1; 1), D= – 36. 4.7. (3; 1; –1). 4.8. (1; –1; 2; –2).

4.9. . 10. . 4.11. (- 3; 2; 4). 4.12. (– 2; 1; 2).

4 .13. (– 3; – 3; 2). 4.14. (4; 0; 1). 4.15. . 4.16. .

4.17. а) X = ; б) X = . 4.18. .

4.19. . 4.20. (- 4; 8; 3).

 

Занятие 5. Метод Гаусса

Изучаемый материал: понятие системы линейных уравнений; виды систем; метод Гаусса решения системы линейных уравнений.

1. Метод Гаусса

5.1 - 5.5

5.6 - 5.10

5.11 - 5.13

 

Решить систему методом Гаусса:

5.1. . 5.2. .

5.3.. 5.4..

5.5..

 

 

Домашнее задание 5

Решить методом Гаусса:

5.6. . 5.7. .

 

5.8.. 5.9..

 

5.10.

 

 

Дополнительное задание 5

Решить методом Гаусса:

5.11. 5.12. 5.13.

. . .

Ответы к занятию 5

5.1. (1/2; 1; 2). 5.2. (1; 0; 2; – 1). 5.3. (1; 5; 2). 5.4. (1; 2; 3; 4).

5.5. (3; 0; – 5; 11). 5.6. (– 2; 0; 1; – 1). 5.7. (3; –2; – 1). 5.8. (2; 3; 5).

5.9. (1; 2; 3; 4). 5.10. (1; 2; – 4; – 3). 5.11. (2; – 1; 3). 5.12. (2; – 2; 3).

5.13. (1; – 1; 0; 1).

 

Занятие 6. Исследование системы линейных уравнений

Изучаемый материал: виды систем линейных уравнений; задача исследования системы линейных уравнений; теорема Кронекера-Капелли; исследование однородной системы.

1. Исследование неоднородной системы	6.1 - 6.3	6.7, 6.8	6.12 - 6.15
2. Исследование однородной системы	6.4, 6.5	6.9, 6.10	6.16 - 6.18
3. Задачи с однородной системой	6.6	6.11	6.19, 6.20

Примечание. Если система совместная и неопределенная, то в качестве свободных неизвестных предпочтительно брать последние неизвестные, а в качестве базовых неизвестных предпочтительно брать первые неизвестные.

 

 

Исследовать систему и в случае совместности найти решение:

6.1. . 6.2. .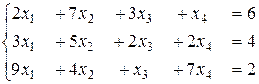

6.3. .

Исследовать однородную систему и в случае существования ненулевого решения найти его:

6.4. 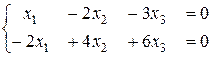. 6.5. .

6.6. При каких значениях параметра a однородная система имеет ненулевое решение?

.