| Вычислить обратную матрицу методом присоединенной матрицы и с помощью элементарных преобразований: |
| |||
| Вычислить ранг матрицы по определению: | 3.10.  . 3.11. . 3.11.  . .
| |||
| Вычислить ранг матрицы методом элементарных преобразований: | 3.12.  . .
| 3.13.  . .
| ||
Дополнительное задание 3
Вычислить обратную матрицу методом элементарных преобразований:
3.14. 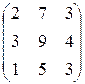 . 3.15.
. 3.15.  . 3.16.
. 3.16.  . 3.17.
. 3.17.  .
.
| Вычислить ранг матрицы по определению: | 3.18. 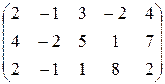 . 3.19. . 3.19.  . .
| ||
| Вычислить ранг матрицы методом элементарных преобразований: | 3.20.  . 3.21. . 3.21.  . .
| ||
Ответы к занятию 3
3.1. 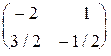 . 3.2.
. 3.2. 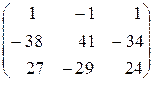 . 3.3. 2. 3.4. 2. 3.5. 1. 3.6. 3.
. 3.3. 2. 3.4. 2. 3.5. 1. 3.6. 3.
3.7.  . 3.8.
. 3.8.  . 3.9.
. 3.9.  .
.
3.10. 2. 3.11. 3. 3.12. 3. 3.13. 3.
3.14. 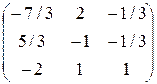 . 3.15.
. 3.15.  . 3.16.
. 3.16.  .
.
3.17.  . 3.18. 2. 3.19. 3. 3.20. 2. 3.21. 2.
. 3.18. 2. 3.19. 3. 3.20. 2. 3.21. 2.
ПосАиГ-П-3-07
Занятие 4. Формулы Крамера. Матричные уравнения
Изучаемый материал: понятие системы линейных уравнений; формулы (правило) Крамера решения системы линейных уравнений; решение матричных уравнений с помощью обратной матрицы.
| 1. Правило Крамера | 4.1, 4.2 | 4.6 - 4.8 | 4.12 – 4.14 |
| 2. Матричные уравнения | 4.3, 4.4 | 4.9, 4.10 | 4.15 – 4.19 |
| 3. Решение системы с помощью обратной матрицы | 4.5 | 4.11 | 4.20 |
Решить системы по правилу Крамера:
4.1. 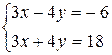 . .
| 4.2. 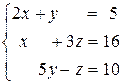 . .
|
Решить матричные уравнения:
4.3. 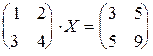 . 4.4. . 4.4.  . .
| ||
| 4.5. Решить систему уравнений с помощью обратной матрицы: | 
|





 . 3.8.
. 3.8.  . 3.9.
. 3.9.  .
.

