2.11.Вычислить:
 . .
| 2.12.Вычислить:
 . .
| 2.13.Вычислить по правилу треугольников: |  . .
|
Вычислить определитель путем разложения по строке или по столбцу:
2.14. 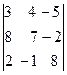 . .
| 2.15. 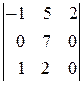 . .
| 2.16.  . .
|
Вычислить определитель с помощью нулей:
2.17.  . .
| 2.18.  . .
| 2.19.  . .
|
Решить уравнение:
2 .20.  . 2.21.
. 2.21.  = 21.
= 21.
Дополнительное задание 2
Вычислить, используя свойства определителей:
2.22. 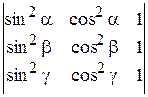 . .
| 2.23.  . .
| |||||
| Вычислить определители: 2.24. 2.25. 2.26. 2.27. | ||||||
 . .
|  . .
| 
| 
| |||
Решить уравнение:
2.28.  = 0. = 0.
| 2.29.  = 0. = 0.
| 2.30. 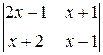 = - 6. = - 6.
| ||
2.31.  = 0. = 0.
| 2.32.  = 0. = 0.
| |||
Ответы к занятию 2
2.1. 18. 2.2. 1. 2.3. 0. 2.4. 0. 2.5. – 2. 2.6. 8 a + 15 b + 12 c – 19 d. 2.7. 0. 2.8. 0.
2.9. 150. 2.10. (2; 3). 2.11. 4 ab. 2.12. 2 a. 2.13.. 0. 2.143. 0. 2.154. –14.
2.165. 2 a – 8 b + c + 5 d. 2.176. 0. 2.187. 48. 2.198. 900. 2.2019. x 1 = – 4, x 2 = – 1.
2.201. x = – 2. 2.221. 0. 2.232 0. 2.243. 100. 2.254. 52. 2.265. 132. 2. 276. – 168.
2.287. 13. 2.298. 1; 2. 2.3029. 1; 5. 2.310. 5. 2.321. – 3, –5/2.
Занятие 3. Обратная матрица. РАНГ МАТРИЦЫ
Изучаемый материал: понятие обратной матрицы; метод присоединенной матрицы вычисления обратной матрицы; элементарные преобразования матриц; эквивалентные матрицы; вычисление обратной матрицы с помощью элементарных преобразований; определение ранга матрицы; вычисление ранга матрицы методом элементарных преобразований.
| 1. Вычисление обратной матрицы | 3.1, 3.2 | 3.7- 3.9 | 3.14 - 3.17 |
| 2. Вычисление ранга матрицы по определению | 3.3, 3.4 | 3.10, 3.11 | 3.18, 3.19 |
| 3. Вычисление ранга матрицы методом элементарных преобразований | 3.5, 3.6 | 3.12, 3.13 | 3.20, 3.21 |
| Вычислить обратную матрицу двумя методами: методом присоединенной матрицы и с помощью элементарных преобразований: | 3.1.  . 3.2. . 3.2. 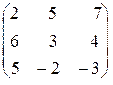 . .
| |
| Вычислить ранг матрицы по определению: | 3.3. 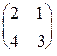 . 3.4. . 3.4. 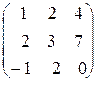 . .
| |
| Вычислить ранг матрицы методом элементарных преобразований: | 3.5.  . 3.6. . 3.6.  . .
| |






