Функция 
называется непрерывной на отрезке 
если а) она непрерывна в любой точке 
а на концах 
и 
отрезка непрерывна справа и слева соответственно, т.е.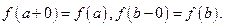 
Функции, непрерывные на отрезке, обладают рядом замечательных свойств, сформулированных ниже.
1. Теорема Вейерштрасса 
Если функция 
непрерывна на отрезке то она ограничена на этом отрезке, т.е. существует постоянная 
такая, что 
2. Теорема Вейерштрасса 
Если функция непрерывна на отрезке то она достигает на этом отрезке своих наибольшего и наименьшего значений, т.е. существуют точки 
такие, что 
3. Теорема Больцано-Коши Если функция непрерывна на отрезке то каково бы ни было значение 
существует значение 
такое, что 
4. Теорема Больцано-Коши Если функция непрерывна на отрезке 
и принимает на концах этого отрезка значения разных знаков 
то существует хотя бы одно значение 
такое, что 
