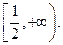Напомним определение монотонных функций.
Определение 1. Говорят, что функция 
строго возрастает на множестве 
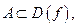если для любых 
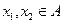из неравенства 
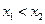вытекает неравенство 
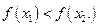Если же 
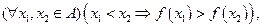то функция называется строго убывающей на множестве 
Если же из строгого неравенства 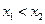между аргументами вытекают нестрогое неравенство 
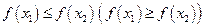между значениями функции, то говорят, что является неубывающей (соответственно невозрастающей) на множестве Множество всех функций строго возрастающих и строго убывающих образует класс строго монотонных функций; невозрастающие и неубывающие функции образует класс просто монотонных функций.
При исследовании на монотонность функций используются выписанная ранее
Теорема Лагранжа. Если функция 
непрерывна на отрезке 
и является дифференцируемой по-крайней мере в интервале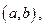 
то существует точка 
такая, что
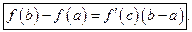
Теорема 1. Пусть функция непрерывна на отрезке и является дифференцируемой по-крайней мере в интервале 
Тогда справедливы следующие высказывания:
1. если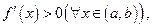 
то функция строго возрастает на отрезке ;
2.если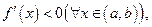 
то функция строго убывает на отрезке .
Доказательство вытекает из равенства (1), в котором надо положить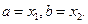 
Действительно, если 
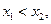а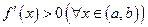 
(тогда и 
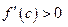), то (см. (1)) будет
выполняться неравенство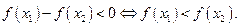 
Это означает, что функция строго возрастает на отрезке . Аналогично доказывается высказывание 2. Теорема доказана.
Замечание 1. Можно показать, что в случае нестрогого знака производной имеет место высказывание:
3. Для того чтобы функция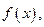 
удовлетворяющая условиям теоремы 1, была неубывающей (невозрастающей) на отрезке , необходимо и достаточно, чтобы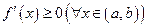 
(соответственно 
).
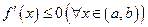Например, функция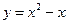 
строго убывает на любом отрезке 
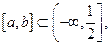так как 
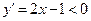при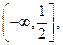 
и эта функция строго возрастает на 
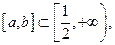так как 
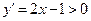при 
