Используя определение 4 производной, а также теоремы 6 и 7, можно доказать следующее утверждение.
Теорема 8. В области определения соответствующих функций имеют место формулы:
Таблица производных
1) 
2) 
3) 
4) 
5) 
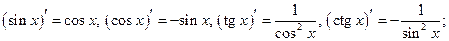
6) 
7) 
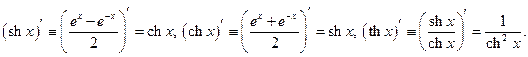
Докажем, например, формулу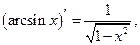 
используя теорему 6 о производной обратной функции. Функция 
является обратной по отношению к функции 
причем 
поэтому по теореме 6 имеем
И, наконец, рассмотрим пример вычисления производной сложной функции, состоящей из многих звеньев:
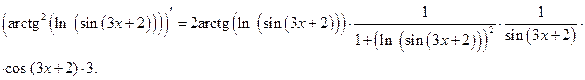
Лекция 3. Логарифмическая производная. Производные и дифференциалы высших порядков. Формула Тейлора с остаточными членами в форме Лагранжа и Пеано. Формулы Маклорена-Тейлора для простейших элементарных функций. Правило Лопиталя. Применение формулы Тейлора
