Мінори й алгебраїчні доповнення

Нехай у визначнику n-го порядку D виділені k різних рядків (k£n) з номерами i₁, i₂, … i_k і стільки ж різних стовпців з номерами j₁, j₂, … j_k... Елементи, розташовані на перетині цих рядків і стовпців, утворюють визначник, що називається мінором k-го порядку і позначається

.

Якщо видалити з визначника рядки і стовпці, що беруть участь у побудові мінору , то елементи, що залишаться, утворять визначник -го порядку, що називається додатковим мінором до і позначається

.

Алгебраїчним доповненням мінору k-го порядку називають величину , де – сума номерів рядків і стовпців, що визначають мінор . Зокрема, мінори першого порядку збігаються з елементами визначника, тому алгебраїчні доповнення першого порядку називають також алгебраїчними доповненнями елементів чи визначника матриці (1.3.9). При цьому . Додатковий мінор (n-1) -го порядку часто називають просто мінором і позначають .

Мінор нульового порядку вважається рівним одиниці, тобто , при цьому додатковий йому мінор і алгебраїчне доповнення збігаються з визначником 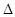. Мінор n-го порядку збігається з визначником 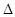, у той час як додатковий до нього мінор і алгебраїчне доповнення вважаються рівними одиниці. Сказане виражається співвідношеннями: ;

Мінори, утворені рядками і стовпцями з однаковими номерами, називають головними (їхні діагональні елементи є і діагональними елементами визначника). Очевидно, визначник n-го порядку має головних мінорів m-го порядку, а всього головних мінорів усіх можливих порядків (від 0 до n).

Якщо мова йде про визначник матриці A, то його мінори k-го порядку позначають:

.

Нехай існує дві чи кілька матриць 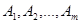однакових порядків. Будемо називати мінори k-го порядку цих матриць 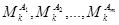взаємно відповідними, якщо вони утворені з цих визначників виявленням рядків і стовпців з тими самими номерами в кожній матриці. Зрозуміло що мінори , додаткові до взаємно відповідних, також є взаємно відповідними.