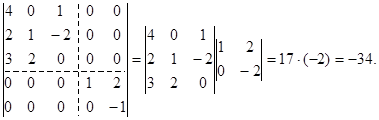Розкласти визначник по елементах рядка чи стовпця простіше всього, коли в цьому рядку чи стовпці мається єдиний ненульовий елемент. Тоді визначник дорівнює добутку цього елемента на його алгебраїчне доповнення. До такого виду можна перетворити визначник шляхом операцій над його рядками чи стовпцями, використовуючи основні властивості (3).
Процес обчислення ілюструється наступним прикладом:
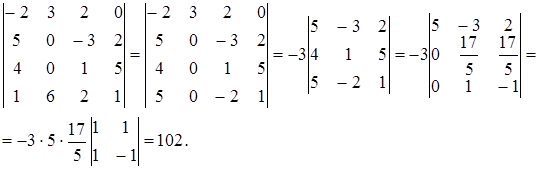
Тут спочатку перший рядок, помножений на (—2), додається до останнього рядка, у результаті чого другий стовпець містить тільки один ненульовий елемент. Розкладання по цьому стовпцю приводить до визначника третього порядку. Додаючи до другого і третього рядків перший, помножений відповідно на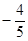 
і —1, одержуємо стовпець з єдиним ненульовим елементом. Тепер розкладаємо визначник по першому стовпцю і зводимо його до визначника другого порядку. Тому що елементи першого рядка виявилися рівними, виносимо за знак визначника множник 
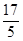і, розкриваючи визначник другого порядку, одержуємо остаточний результат D = 102.
Найбільш просто обчислюється визначник трикутної чи діагональної матриці: він дорівнює добутку діагональних елементів. Це випливає з розкладання по елементах стовпців (рядків) визначника верхньої (нижньої) трикутної матриці (у випадку діагональної матриці розкладання можна виконувати по елементах рядків чи стовпців). Значення визначників трикутних матриць не залежать від елементів, розташованих поза головною діагоналлю.
Приклад 1-22:
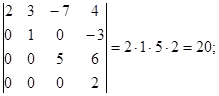
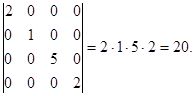
За допомогою розкладання Лапласа можна також показати, що визначник квазідіагональної матриці дорівнює добутку визначників квадратних матриць, розташованих уздовж головної діагоналі:
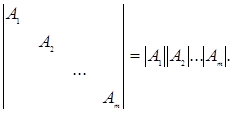
Дійсно, розкладаючи визначник по елементах рядків матриці А1, одержуємо єдиний ненульовий мінор, що збігається з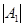 
, і т.д.
Приклад 1-23:
