Перетворення матриці A, що складається в заміні рядків стовпцями (чи стовпців рядками) при збереженні їхньої нумерації, називається транспонуванням. Отримана в результаті такого перетворення матриця називається транспонованої до матриці A і 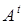 чи позначається
чи позначається  :
:
| A= | a11 | a12 | … | a1n | ; 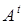 = =
| a11 | a12 | … | am1 | |
| a21 | a22 | … | a2n | a21 | a22 | … | am2 | |||
| … | … | … | … | … | … | … | … | |||
| am1 | am2 | … | amn | a1n | a2n | … | anm |
Довільна  - матриця при транспонуванні стає
- матриця при транспонуванні стає  -матрицею, а елемент Aij займає ij-клітку, тобто aij =
-матрицею, а елемент Aij займає ij-клітку, тобто aij =  .
.
Якщо матриця (квадратна) збігається зі своєю транспонованою, тобто  , то вона називається симетричною і її елементи зв'язані співвідношенням
, то вона називається симетричною і її елементи зв'язані співвідношенням  (симетрія щодо головної діагоналі). Матриця, для якої A=-At, називається кососиметричною, і її елементи зв'язані співвідношенням
(симетрія щодо головної діагоналі). Матриця, для якої A=-At, називається кососиметричною, і її елементи зв'язані співвідношенням  . Вона, як і симетрична матриця, завжди квадратна, але діагональні елементи дорівнюють нулю, тобто
. Вона, як і симетрична матриця, завжди квадратна, але діагональні елементи дорівнюють нулю, тобто 
 . Нижче приведені приклади симетричної і кососиметричної матриць:
. Нижче приведені приклади симетричної і кососиметричної матриць:
| 0,5 | -5 | 0,1 | ||||||
| 0,5 | -2 | -3 | ||||||
| 0,1 | -0,1 | -7 | ||||||
| -5 | -4 |
Ясно, що не всі елементи таких матриць можуть бути обрані довільно. Можна переконатися, що з  елементів для симетричної матриці незалежними можуть бути тільки
елементів для симетричної матриці незалежними можуть бути тільки 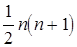 , а для кососиметричної -
, а для кососиметричної -  елементів.
елементів.
Комплексно-сполучена і транспонована матриця 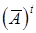 називається сполученою з А и позначається через А*. Матриця, рівна своїй сполученій, тобто А =
називається сполученою з А и позначається через А*. Матриця, рівна своїй сполученій, тобто А = 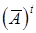 = А*, називається ермітовой. Якщо A=
= А*, називається ермітовой. Якщо A=  , то А — косоермітова матриця.
, то А — косоермітова матриця.
Легко показати, що транспонування добутку АВ дорівнює добутку транспонованих матриць, узятих у зворотному порядку:  . Двічі транспонована матриця дорівнює початковій, тобто
. Двічі транспонована матриця дорівнює початковій, тобто 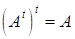 .
.
2.1.7. МАТРИЧНИЙ ЗАПИС СИСТЕМИ ЛІНІЙНИХ РІВНЯНЬ.
Спочатку матриці були введені для спрощення запису систем лінійних рівнянь, що обумовило і визначення основних матричних операцій. Система лінійних рівнянь:
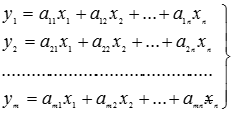
записується однією матричною рівністю
| y1 | = | a11 | a12 | … | a1n | x1 | |
| y2 | a21 | a22 | … | a2n | x2 | ||
| … | … | … | … | … | … | ||
| ym | am1 | am2 | … | amn | xn |
Дійсно, перемноживши в правій частині рівності (m x n) - матрицю на стовпцеву матрицю, одержимо

| = | a11x1+ a12x2+…….+ a1nxn |

| a21x1+ a22x2+…….+ a2nxn | |
| … | ............................ | |

| am1x1+ am2x2+…….+ amnxn |
З рівності матриць-стовпців випливають рівності для відповідних елементів, що збігаються з вихідною системою рівнянь. Якщо позначити
| y = | y1 | ; A = | a11 | a12 | … | a1n | ; x = | x1 |
| y2 | a21 | a22 | … | a2n | x2 | |||
| … | … | … | … | … | … | |||
| ym | am1 | am2 | … | amn | xn |
то матрична рівність запишеться ще коротше

Таке представлення системи лінійних рівнянь виявилося можливим завдяки правилу множення матриць, що щонайкраще підходить для цієї мети. Однак історично справа обстояла саме навпаки: правила дій над матрицями визначалися, насамперед, виходячи зі зручності представлень систем лінійних рівнянь.
2.1.8. ЛІНІЙНІ ПЕРЕТВОРЕННЯ.
Систему рівнянь, записану на початку попереднього пункту, можна розглядати як лінійне перетворення сукупності величин x1,x2,..xn у сукупність y1,y2,..,ym. Це перетворення цілком визначається коефіцієнтами 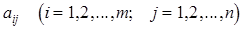 . мовою матриць лінійне перетворення
. мовою матриць лінійне перетворення  означає перетворення стовпця x у стовпець
означає перетворення стовпця x у стовпець  , що визначається матрицею перетворення А.
, що визначається матрицею перетворення А.
Нехай величини x1,x2,..xn виходять з деякої сукупності величин z1,z2...,zr, за допомогою лінійного перетворення 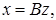 де x і z — стовпці відповідних величин; В — матриця їхнього перетворення. Тоді формальною підстановкою x у перше матричне рівняння одержуємо
де x і z — стовпці відповідних величин; В — матриця їхнього перетворення. Тоді формальною підстановкою x у перше матричне рівняння одержуємо

де С = АВ — матриця перетворення величин z в. До цього ж результату можна прийти шляхом підстановки значень x1,x2,..xn із другої системи рівнянь у першу з обліком уведеного раніше правила множення прямокутних матриць.
2.1.9. ЗВОРОТНЯ МАТРИЦЯ.
У звичайній алгебрі два числа, добуток яких дорівнює одиниці, називають взаємно зворотними. Число, зворотне числу  , позначається через
, позначається через  і по визначенню
і по визначенню  . Аналогічно в матричній алгебрі дві квадратні матриці, добуток яких дорівнює одиничній матриці, тобто
. Аналогічно в матричній алгебрі дві квадратні матриці, добуток яких дорівнює одиничній матриці, тобто  , називають взаємно зворотними (A зворотня A-1). Однак далі цього аналогія не проходить.
, називають взаємно зворотними (A зворотня A-1). Однак далі цього аналогія не проходить.
Вираження  , де
, де  і
і  — числа, можна представити як частка від розподілу
— числа, можна представити як частка від розподілу  на
на  , але для матриць таке представлення не має змісту й у загальному випадку
, але для матриць таке представлення не має змісту й у загальному випадку  Тому замість операції розподілу B на A розрізняють ліве приватне
Тому замість операції розподілу B на A розрізняють ліве приватне  і праве часткове
і праве часткове  ,що зводяться до множення ліворуч чи праворуч на зворотну матрицю
,що зводяться до множення ліворуч чи праворуч на зворотну матрицю 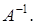
Спосіб звертання матриці найпростіше установити, розглядаючи рішення системи n лінійних рівнянь з n невідомими:
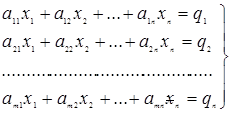
У матричній формі ця система рівнянь запишеться як  , де
, де  квадратна матриця n-го порядку, називана матрицею системи; x і q cтовпцеві матриці невідомих змінних і вільних членів:
квадратна матриця n-го порядку, називана матрицею системи; x і q cтовпцеві матриці невідомих змінних і вільних членів:
| A = | a11 | a12 | … | a1n | ; x = | x1 | ; q = | q1 |
| a21 | a22 | … | a2n | x2 | q2 | |||
| … | … | … | … | … | … | |||
| am1 | am2 | … | amn | xn | qn |
Матричне рівняння  урівнюється множенням обох його частин ліворуч на зворотну матрицю
урівнюється множенням обох його частин ліворуч на зворотну матрицю  , тобто A-1Ax = A-1q, у результаті чого одержуємо
, тобто A-1Ax = A-1q, у результаті чого одержуємо  .
.
Відповідно до правила Крамера невідомі xk (k=1,2,…,n) визначаються співвідношенням:

де 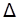 — визначник системи рівнянь у
— визначник системи рівнянь у  — алгебраїчні доповнення.
— алгебраїчні доповнення.
Визначник (являє собою числову функцію, що обчислюється за визначеними правилами на підставі квадратної таблиці, що складає з коефіцієнтів системи рівнянь
| D = | а 11 | а 12 | ... | а 1n |
| а 21 | а 22 | ... | а 2n | |
| ... | ... | ... | ... | |
| а n1 | а n2 | ... | а nn |
Табличне представлення визначника D за формою збігається з матрицею системи рівнянь, тобто складається з тих же елементів і в тім же порядку, що і матриця А. У таких випадках його називають визначником матриці А и записують D = det.
Алгебраїчне доповнення Dsk обчислюється як визначник матриці, отриманої видаленням з матриці A s-го рядка і k-го стовпця, причому цей визначник збільшується ще на  . Величину Dsk називають також алгебраїчним доповненням елемента а sk матриці A. Часто визначник матриці A позначається через | A |, а алгебраїчне через А sk .
. Величину Dsk називають також алгебраїчним доповненням елемента а sk матриці A. Часто визначник матриці A позначається через | A |, а алгебраїчне через А sk .
Записавши для всіх елементів стовпцевої матриці х вираження за правилами Крамера, одержимо рішення системи рівнянь у виді:
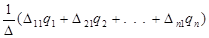 x 1 x 1
| = | D11 | D21 | ... | Dn1 | q1 | |||
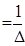 x 2 x 2
| 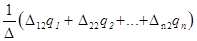
| D12 | D22 | ... | Dn2 | q2 | |||
 ... ...
| ............... | ... | ... | ... | ... | ... | |||
| x n | D1n | D2n | ... | Dnn | qn |
відкіля, порівнюючи з  , маємо
, маємо
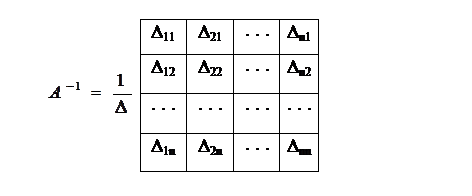 |
З отриманого вираження випливає правило визначення зворотної матриці: 1) елементи aij даної матриці А n-го порядку заміняються їх алгебраїчними доповненнями Dij; 2) матриця алгебраїчних доповнень транспонується, у результаті чого одержуємо приєднану чи взаємну матрицю до А (вона позначається через Adj); 3) обчислюється визначник D матриці А и приєднана матриця Adj збільшується на величину, зворотню цьому визначнику. Зворотня матриця існує для матриці А за умови, що det¹0. Такі матриці називаються неособливими, на відміну від особливих (випороджених), визначник яких дорівнює нулю. Нижче обчислення зворотної матриці ілюструється прикладом:
| -28 | -38 | -12 | |||||
 -3 -3
| ® | -2 | -13 | ® | |||
| -5 | -1 | -14 |
detA=-94 (1)
| -28 | 
| 
| 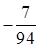
| |||||
| ® | -38 | -2 | -14 | ® | 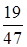
| 
| 
| = 
|
| -12 | -13 | |||||||
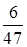
| 
| 
| ||||||
| (2) |
(3)
Матриця, зворотня добутку двох матриць, дорівнює переставленому добутку матриць, зворотніх вихідним, тобто 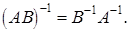 Дійсно, помноживши обидві частини цієї рівності на
Дійсно, помноживши обидві частини цієї рівності на  , приходимо до тотожності
, приходимо до тотожності  , тому що
, тому що  , де Е – одинична матриця n-го порядку.
, де Е – одинична матриця n-го порядку.






