ѕон€тт€ визначника (детерм≥нанта) виникло у зв'€зку з р≥шенн€м систем л≥н≥йних р≥вн€нь ≥ завд€ки цьому ц€ задача одержала компактне вираженн€, наприклад, у вигл€д≥ правила рамера (2.1.9.). ѕредставленн€ таких систем у матричн≥й форм≥  природним образом зв'€зуЇ квадратну матрицю
природним образом зв'€зуЇ квадратну матрицю  з њњ визначником
з њњ визначником 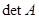 (чи
(чи  ). «агальне вираженн€ дл€ визначника матриц≥ n-го пор€дку звичайно даЇтьс€ у вигл€д≥:
). «агальне вираженн€ дл€ визначника матриц≥ n-го пор€дку звичайно даЇтьс€ у вигл€д≥:
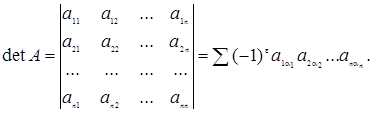
” прав≥й частин≥ стоњть сума добутк≥в виду 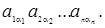 ожен такий добуток за визначенн€м повинен м≥стити елементи матриц≥
ожен такий добуток за визначенн€м повинен м≥стити елементи матриц≥  , розташован≥ в р≥зних р€дках ≥ р≥зних стовпц€х. ÷е означаЇ, що серед ус≥х перших ≥ндекс≥в, €к ≥ серед ус≥х других ≥ндекс≥в не повинне бути однакових. якщо розташувати перш≥ ≥ндекси в пор€дку њхнього зростанн€, €к це зроблено вище, то сукупн≥сть других ≥ндекс≥в утворить де€ку перестановку
, розташован≥ в р≥зних р€дках ≥ р≥зних стовпц€х. ÷е означаЇ, що серед ус≥х перших ≥ндекс≥в, €к ≥ серед ус≥х других ≥ндекс≥в не повинне бути однакових. якщо розташувати перш≥ ≥ндекси в пор€дку њхнього зростанн€, €к це зроблено вище, то сукупн≥сть других ≥ндекс≥в утворить де€ку перестановку 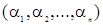 множини чисел в≥д 1 до n. ≤накше кажучи, кожен добуток п≥д знаком суми визначаЇтьс€ п≥дстановкою n-го ступен€:
множини чисел в≥д 1 до n. ≤накше кажучи, кожен добуток п≥д знаком суми визначаЇтьс€ п≥дстановкою n-го ступен€:
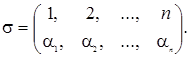
„исло вс≥х п≥дстановок n-го ступен€ дор≥внюЇ n!, тому можна утворити таку ж к≥льк≥сть добутк≥в 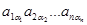 з елемент≥в даноњ матриц≥ (при нульових елементах де€к≥ з них дор≥внюють нулю). ¬изначник дор≥внюЇ сум≥ вс≥х таких добутк≥в, уз€тих з≥ знаком (Ч1)e, де e Ч число ≥нверс≥й перестановки
з елемент≥в даноњ матриц≥ (при нульових елементах де€к≥ з них дор≥внюють нулю). ¬изначник дор≥внюЇ сум≥ вс≥х таких добутк≥в, уз€тих з≥ знаком (Ч1)e, де e Ч число ≥нверс≥й перестановки  . «ам≥сть множника (Ч1)e можна писати знак п≥дстановки sgns, що позитивний дл€ парноњ ≥ негативний дл€ непарноњ п≥дстановки s.
. «ам≥сть множника (Ч1)e можна писати знак п≥дстановки sgns, що позитивний дл€ парноњ ≥ негативний дл€ непарноњ п≥дстановки s.
ѕор€док визначника зб≥гаЇтьс€ з пор€дком його матриц≥. ≈лементи  матриц≥ ј називають також елементами визначника
матриц≥ ј називають також елементами визначника  , а добутку (Ч1)e
, а добутку (Ч1)e 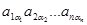 Ч членами визначника.
Ч членами визначника.
ƒл€ визначник≥в другого ≥ третього пор€дку одержуЇмо вираз, що зб≥гаЇтьс€ з добре в≥домими схемами обчисленн€ цих визначник≥в:
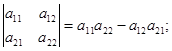

як видно, ≥ндекси стовпц≥в ус≥х член≥в визначника третього пор€дку визначаютьс€ перестановками (1,2,3), (2,3,1), (3,1,2), (3,2,1), (1,3,2), (2,1,3), число ≥нверс≥й €ких дор≥внюЇ в≥дпов≥дно 0, 2, 2, 3, 1, 1.
«агальне вираженн€ визначника n-го пор€дку Ї зручним дл€ досл≥дженн€ ≥ доказу його властивостей, але дл€ обчисленн€ визначник≥в використовуютьс€ ≥нш≥ б≥льш практичн≥ сп≥вв≥дношенн€ ≥ методи.






