Визначник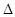 
n-го порядку виражається через елементи довільного його рядка чи стовпця в такий спосіб:
,
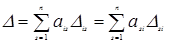
де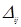 
– алгебраїчне доповнення елемента 
(1.3.9). Ці співвідношення дозволяють представити визначник n-го порядку через визначники (n -1)-го порядку. При обчисленнях доцільно розкладати визначник по рядку, чи по стовпцю, що має більшу кількість нульових елементів. Наприклад, розкладаючи даний визначник по елементах другого стовпця, маємо:
.
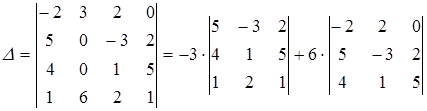Розкладаючи визначники третього порядку, одержуємо:
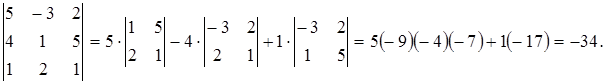
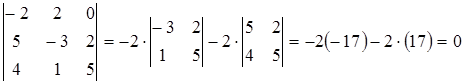
Другий визначник виявився рівним нулю, тому що його третій стовпець дорівнює сумі першого і другого (властивість 2). Таким чином, знаходимо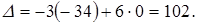 
Узагальненням викладеного методу є розкладання Лапласа по декільком рядкам чи стовпцям. Нехай задані будь-які k рядків (чи стовпців) визначника 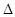. Тоді цей визначник можна представити як суму добутків деяких мінорів k-го порядку, розташованих у цих рядках (чи стовпцях) на їхні алгебраїчні доповнення, тобто
,
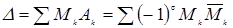де s — сума номерів рядків і стовпців, що беруть участь у формуванні мінору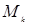 
(чи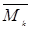 
,). Очевидно, число доданків у цій сумі дорівнює 
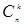(деякі з них можуть дорівнювати нулю). Наприклад, розкладаючи приведений вище визначник по першому і другому стовпцях, маємо:
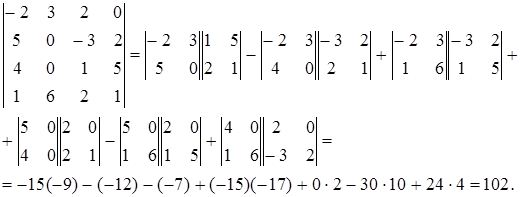
Приведені співвідношення рідко використовуються безпосередньо для обчислення визначників, але вони надзвичайно корисні при обґрунтуванні різних методів. Приведемо також вираз, що узагальнює розкладання по елементах рядка чи стовпця:
