По визначенню добутком матриці А на число a (на відміну від матриць і векторів, числа часто називають скалярами) є матриця С = a А, елементи якої виходять множенням відповідних елементів матриці А на це число а, тобто приклад 
:
| 2 * | -1 | = | -2 | |||||
Очевидно, справедливі наступні співвідношення: a (А +В)= aA+aB; (ab)A=a(bA) де А и В — матриці однакового розміру; a і b — числа (скаляри). Загальний множник елементів можна виносити за знак матриці, вважаючи його скалярним множником.
Різниця двох матриць однакових розмірів зводиться до вже розглянутих операцій співвідношенням А — В =А+(-1)В,. тобто С = А — В, якщо 
.
2.1.5. МНОЖЕННЯ МАТРИЦЬ.
По багатьом розумінням доцільно визначити цю операцію в такий спосіб: добутком матриці А розміру 
на матрицю В розміру 
є матриця С = АВ розміру , елемент 
якої, розташований у 
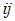-клітці, дорівнює сумі добутків елементів i-й рядка матриці А на відповідні елементи j-го стовпця матриці В, тобто
cij = ai1b1j + ai2b2j + … + ainbnj = 
Множення А на В припустимо (добуток АВ існує), якщо число стовпців A дорівнює числу рядків B (у таких випадках говорять, що ці дві матриці погодяться за формою). Приклад:
| = | 2*1+0*2+3*4+1*3 | 2*3+0*1+3*0+1*5 | = | ||||||||
| 5*1+1*2+2*4+0*3 | 5*3+1*1+2*0+0*5 | ||||||||||
| 0*1+0*2+4*4+1*3 | 0*3+0*1+4*0+1*5 | ||||||||||
| = | ||
Для матриць А и В існує як добуток АВ розміру 
, так і добуток ВА розміру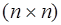 
. Ясно, що при 
ці добутки не можуть бути рівними вже внаслідок різних розмірів результуючих матриць. Але навіть при 
, тобто у випадку квадратних матриць однакового порядку, добутку АВ і ВА не обов'язково рівні між собою. Наприклад, для матриць
| А= | -1 | ; | В= | ; | |||
маємо
| АВ= | ; | ВА= | - 3 | ; | |||
| -2 |
Звідси випливає, що взагалі операція множення матриць не підкоряється комутативному закону (АВ 
ВА). Якщо ж виконується співвідношення АВ = ВА, то матриці А и В називають комутірующими чи перестановчими. Асоціативний і дистрибутивний закони для матричного множення виконуються у всіх випадках, коли розміри матриць допускають відповідні операції: (АВ)С = А(ВС) = АВС (асоціативність), А+(В+С) = АВ+АС і (А — В)С = АС - ВС (дистрибутивність множення ліворуч і праворуч щодо додавання).
Множення - матриці А на одиничну матрицю т-го порядку ліворуч і на одиничну матрицю n-го порядку праворуч не змінює цієї матриці, тобто 
. Якщо хоча б одна з матриць добутку АВ є нульовий, то в результаті одержимо нульову матрицю.
Відзначимо, що з 
не обов'язково випливає, що 
чи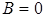 
. У цьому можна переконатися на наступному прикладі:
| ´ | = | ||||||
| 0,5 | -4 | ||||||
