Перестановки з повтореннями

Поставимо таке питання. Скількома способами можна розкласти множину А, що складається з n елементів, на суму m підмножин 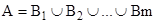так, щоб , де — дані числа ? Множини 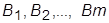не повинні мати спільних елементів.

Всі описані вище розбиття множини А на m груп 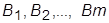можна дістати так: візьмемо довільну -елементну підмножину В₁, множини А (це можна зробити способами); серед елементів, що залишились, візьмемо -елементну підмножину (це можна зробити способами) і т.д. Загальне число способів вибору різних множин 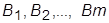за правилом множення дорівнює

ТЕОРЕМА 1.8. Число різних перестановок, які можна утворити з n елементів, серед яких є елементів першого типу, елементів другого типу, …, 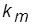елементів m- го типу, дорівнює

(1.6)

Числа називають поліномними коефіцієнтами.

1.4.5. ВЗАЄМНО ОДНОЗНАЧНА ВІДПОВІДНІСТЬ.

Припустимо, що задано дві множини А і B. Вважатимемо, що між цими множинами встановлено відповідність, якщо кожному елементу а з А відповідає деякий елемент b з В і для кожного елемента b з В існує такий елемент а з А, що b відповідає а. Ця відповідність буде взаємно однозначною, якщо кожному елементу з А відповідає лише один елемент з В і різним елементам множини А відповідають різні елементи В.

Приклад 1-17. А — множина учнів класу, В — множина парт, кожному учневі відповідає парта, за якою він сидить (це не взаємно однозначна відповідність).
Приклад 1-18. Прикладом взаємно однозначної відповідності може бути відповідність між елементами впорядкованої множини з n елементами і числами 1,2,...,n; кожному елементу відповідає його номер.

Множини, для яких існує взаємно однозначна відповідність, називаються еквівалентними.

ТЕОРЕМА 1.9. Для того, щоб дві множини були еквівалентними, необхідно і достатньо, щоб вони мали однакову кількість елементів.

Доведення. Якщо множини А і В мають однакову кількість елементів n, то, впорядковуючи кожну з них певним чином і ставлячи у відповідність k-му елементу множини k-й елемент множини 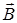, дістанемо взаємно однозначну відповідність між множинами А і В, тобто А \ В еквівалентні.

Припустимо тепер, що А має n елементів, і існує взаємно однозначна відповідність між множинами А і В. Впорядкуємо множину А: нехай елементи А — це Позначимо через той елемент B, який відповідає . Оскільки кожному елементу з А відповідає елемент з B, різним елементам А відповідають різні елементи В і кожен елемент з В відповідає деякому елементу з A, то В складається з елементів отже, В має n елементів.

НАСЛІДОК. Якщо дві множини еквівалентні, то вони мають однакову кількість елементів.

Цю властивість еквівалентних множин дуже часто використовують для обчислення кількості елементів різних множин. Використовуючи попередній приклад, можемо сказати, що шукане число розміщень буде .

1.4.6. КОМБІНАЦІЇ З ПОВТОРЕННЯМИ.

Комбінаціями з m елементів по n елементів з повтореннями називаються групи, що містять n елементів, причому кожен елемент належить до одного з m типів.

Приклад 1-19. З трьох елементів а, b, с можна утворити такі комбінації по два з повтореннями:

ТЕОРЕМА 1.10. Число різних комбінацій з m елементів по n дорівнює

Доведення. Кожна комбінація повністю визначається, якщо вказати, скільки елементів кожного з m типів в неї входить. Поставимо у відповідність кожній комбінації послідовність з нулів та одиниць, утворену за таким правилом: напишемо підряд стільки одиниць, скільки елементів першого типу входить в комбінацію, далі поставимо нуль і після нього напишемо стільки одиниць, скільки елементів другого типу містить ця комбінація, і т. д. Наприклад, написаним вище комбінаціям з трьох по два будуть відповідати такі послідовності:

Таким чином, кожній комбінації з m по n відповідає послідовність з n одиниць та m—1 нулів і, навпаки, за кожною такою послідовністю однозначно відновлюється така комбінація. Тому число комбінацій з m по n з повтореннями дорівнює числу послідовностей з n одиниць та m — 1 нулів, тобто дорівнює .

Приклад 1-20. Кості доміно можна розглядати як комбінації з повтореннями по два з семи цифр 0, 1,2, 3, 4, 5, 6. Число всіх таких комбінацій дорівнює

Приклад 1-21. Скільки цілих невід'ємних розв'язків має рівняння

Існує тісний зв'язок між розв'язками вказаного рівняння та комбінаціями з m елементів по n. Якщо маємо невід'ємні цілі числа 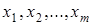такі, що 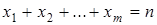, то можемо утворити комбінацію з m елементів по n, взявши 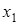елементів першого типу, — другого,..., — m -го типу. Навпаки, маючи комбінацію з m елементів по n, дістанемо розв'язок рівняння 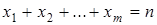( 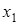елементів першого типу, — другого,..., — m -го типу) в цілих невід'ємних числах. Отже, між множиною всіх комбінацій з m елементів по n з повтореннями та множиною всіх невід'ємних цілих розв'язків рівняння 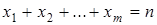встановлюється взаємно однозначна відповідність. Тому число розв'язків дорівнює .

1.4.7. БІНОМ НЬЮТОНА.

Відомо, що

(1.7)

Як розкрити дужки при обчисленні виразу ? Відповідь на це питання дає така теорема.

ТЕОРЕМА 1.11. Має місце рівність:

(1.8)

Цю теорему іноді називають біномною теоремою, а числа біномними коефіцієнтами. Рівність (1.8) називають часто біномом Ньютона, причому ця назва з точки зору історії не є справедливою, бо формулу для знали ще середньоазіатські математики Омар Хайям, Гіяседін. В Західній Європі до Ньютона її знав Паскаль (1623—1662). Заслуга Ньютона в тому, що він узагальнив формулу (1) для нецілого показника n. Нагадаємо, що є число k-елементних підмножин у множині з n елементів. Формулу (1) можна записати у вигляді:

Доведення. Перемножимо послідовно раз. Тоді одержимо суму 2ⁿ доданків виду де () дорівнює або a, або b. Розіб'ємо всі доданки на (n + 1) групу віднісши до всі ті доданки, в яких b зустрічається множником k раз, а a — (n-k), раз. Число доданків у дорівнює, очевидно, (таким числом способів серед n множників можна вибрати k множників, які дорівнюватимуть b), а кожен доданок в дорівнює 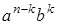. Тому

Теорему доведено.

Нагадаємо таку важливу властивість біномних коефіцієнтів

, (1.9)

Рівність (2) показує, що біномні коефіцієнти можна послідовно виписувати у вигляді трикутної таблиці, яка називається трикутником Паскаля:

В n-му рядку трикутника Паскаля стоять коефіцієнти розкладу , причому кожен коефіцієнт, крім крайніх двох, які дорівнюють Г, дорівнює сумі відповідних коефіцієнтів з попереднього рядка.