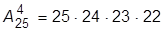1.4.1. ПРАВИЛО СУМИ І ДОБУТКУ
ТЕОРЕМА 1.2. (Правило суми)
Якщо об’єкт а може бути обрано р способами, а об’єкт b – другими q способами, то вибір “або а або b ” може бути виконаю p+q способами.
При цьому слід мати на увазі, що вибір а і b є тут взаємно виключним.
Інакше кажучи, необхідно слідкувати, щоб ні один зі способів вибору об’єкта а не співпадав з якимсь зі способів вибору об’єкта b. При наявності таких обмеженостей правило суми не працює і результат дорівнює p+q-k.
ТЕОРЕМА 1.3. (Правило множення)
Якщо об’єкт а може бути обрано р способами і після кожного з таких виборів об’єкт b може бути в свою чергу обрано q способами, то вибір “ а і b ” у вказаному порядку можливо здійснити p*q способами.
Це правило використовується в тих випадках, коли вибір а і в незалежний.
Приклад 1-13. Скільки чотиризначних чисел можна скласти з цифр 0, 1, 2, 3, 4, 5, якщо жодна цифра не повторюється більше одного разу?
Розв'язання. Першою цифрою числа може бути одна з 5 цифр 1, 2, 3,4,5 (0 не може бути, бо тоді число не чотиризначне); якщо перша цифра обрана, то друга може бути обрана 5 способами, третя — 4, четверта — 3. Згідно з правилом множення загальне число способів дорівнює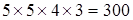 
.
1.4.2. ПІДМНОЖИНИ ДАНОЇ МНОЖИНИ.
Якщо задана деяка множина А, то можна розглядати нову множину М(А) – множину всіх її підмножин. Через Мk(А) будемо позначати множину всіх підмножин А, які мають k елементів: ВÎМk(А), якщо ВÎМ(А) і N(B) = k.
ТЕОРЕМА 1.3. Число всіх k – елементних підмножин множини з n елементів дорівнює
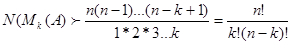(1.1)
N(Mk(A)) позначимо через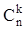 
.
Довільна k елементна підмножина n – елементної множини називається сполукою (комбінацією) з n елементів по k. Порядок елементів в підмножині не є істотним. Таким чином, число комбінацій (сполук) із n елементів по k дорівнює
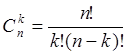(1.2)
Приклад 1-14. Скількома способами читач може відібрати 3 книжки з 5?
Розв’язок. Шукане число способів дорівнює числу трьохелементних
підмножин множини з 5 елементів: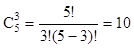 
.
ТЕОРЕМА 1.4. Має місце рівність:
Cnk = Ckn-1+Cn-1k-1 (1.3)
Доведення виконується за допомогою формули (1.1).
ТЕОРЕМА 1.5. Число всіх підмножин множини з n елементів дорівнює 2n.
Доведення. Пронумеруємо елементи множини А і для кожної підмножини А побудуємо послідовність довжини n з нулів та одиниць. Таким чином:
на k-му місті пишемо 1, якщо елемент з номером k входить до підмножини. Отже кожній підмножині відповідає своя послідовність нулів та одиниць. Наприклад, порожній множині відповідає послідовність з одних нулів. Число всіх можливих послідовностей довжини n, складених з нулів та одиниць дорівнює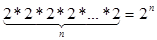 
. Отже число всіх підмножин множини А дорівнює 2n.
НАСЛІДОК ТЕОРЕМИ. Має місце рівність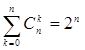 
.
Оскільки Сnk – число k елементних підмножин множини з n елементів, то сума в лівій частині є число всіх підмножин.
1.4.3. ВПОРЯДКОВАНІ МНОЖИНИ. ПЕРЕСТАНОВКИ
І РОЗМІЩЕННЯ
Множина називається впорядкованою, якщо кожному елементу цієї множини поставлено у відповідність певне число (номер елемента) від 1 до n, де n — число елементів множини, так що різним елементам відповідають різні числа. Кожну скінчену множину можна перетворити у впорядковану, якщо, наприклад, переписати всі елементи множини у деякий список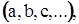 
а потім поставити у відповідність кожному елементу номер місця, на якому він стоїть у списку Будемо позначати впорядковану множину, яка утворена з множини А через 
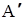. Очевидно, що кожну множину, яка містить більше одного елемента, можна впорядкувати не одним способом.
Впорядковані множини вважаються різними, якщо вони відрізняються або своїми елементами, або їх порядком. Різні впорядковані множини, які відрізняються лише порядком елементів (тобто можуть бути утворені з тієї самої множини), називаються перестановками цієї множини.
Приклад 1-15. Перестановки множини А = (а, b, с) з трьох елементів мають вигляд:
(а, b, с), (а, с, b), (b, а, с),
(b, с, а), (с, а, b), (с, b, а).
Знайдемо кількість різних способів, якими може бути впорядкована дана множина, тобто кількість перестановок множини А. Нехай множина А має n елементів.
ТЕОРЕМА 1.6. Кількість перестановок множини з n елементів позначається через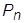 
і дорівнює
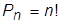
Доведення. Будемо послідовно вибирати елементи множини А і розташовувати їх у певному порядку на n місцях На перше місце можна поставити будь-який з n елементів Після того, як заповнено перше місце, на друге місце можна поставити будь-який з тих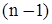 
елементів, які
залишились, і т д. За правилом множення всі n місць можна заповнити
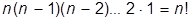
способами. Отже, множину А з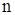 
елементів можна впорядкувати 
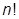способами.
Приклад 1-16. Скількома способами можна розташувати на полиці 4 книги (позначимо їх А, В, С, D)?
Шукане число способів дорівнює числу способів упорядкування множини, що складається з 4 елементів, тобто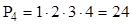 
.
Розглянемо тепер впорядковані підмножини даної множини А. Саму множину А вважаємо невпорядкованою, тому кожна її підмножина може бути впорядкована будь-яким можливим способом. Число всіх підмножин множини А з k елементами дорівнює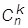 
. Кожну таку підмножину можна впорядкувати 
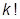способами. Так знайдемо всі впорядковані n-елементні підмножини множини. Отже, їх число буде 
.
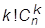ТЕОРЕМА 1.7. Число впорядкованих k елементних підмножин множини, що складається з n елементів, дорівнює
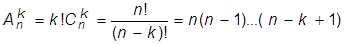(1.4)
Упорядковані k-елементні підмножини множини з n елементів називають розміщеннями з n по k. Різні розміщення з n по k відрізняються складом елементів, або їх порядком.
Отже, число різних розміщень з n по k дорівнює
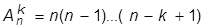(1.5)
Приклад 1-16. Скількома способами можна розсадити 4 учнів на 25 місцях?
Шукане число дорівнює числу розміщень з 25 по 4 
