Усяке функціональне відношення можна розглядати як функцію. При цьому перша координата х упорядкованої пари 
є аргументом (перемінною), а друга 
— образом (значенням) функції. Звичайний запис у=f(x) відповідає співвідношенню xfy, або 
. Варто розрізняти функцію f як множину упорядкованих пар (відношення) і значення функції 
як другу координату однієї з таких пар.
Для усякого функціонального відношення А можна визначити зв'язану з цим відношенням функцію f. Але симетричне до нього відношення 
може і не бути функцією. Так, відношення
,
зворотне розглянутому в (1), не є функцією.
Якщо функціональне відношення 
усюди визначене на X, тобто його область визначення 
збігається з множиною X, то його називають відображенням множини Х в Y і записують
Відображення можна також розглядати як функцію f, визначену на множині Х і яка приймає значення в множині Y.
Як видно, різниця між відображенням і функцією зводиться до способу визначення цих відношень на множині X, причому відображення варто розглядати як окремий випадок функції. Однак більшість авторів не розрізняють поняття відображення і функції, залишаючи відкритим питання про область визначення. Якщо f - відображення або функція, то пишуть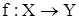 
або простіше 
.
