При відображенні Х в Y кожний елемент x із Х має один і тільки один образ 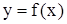 із Y. Однак зовсім не обов'язково, щоб і всякий елемент із Y був образом деякого елемента з Х (мал. 1.10, а). Якщо ж будь-який елемент із Y є образ, принаймні, одного елемента з Х (мал. 1.10, б), то говорять, що має місце відображення Х на Y - «сюр’єкция» або накриття.
із Y. Однак зовсім не обов'язково, щоб і всякий елемент із Y був образом деякого елемента з Х (мал. 1.10, а). Якщо ж будь-який елемент із Y є образ, принаймні, одного елемента з Х (мал. 1.10, б), то говорять, що має місце відображення Х на Y - «сюр’єкция» або накриття.
Якщо для будь-яких двох різних елементів 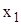 і
і 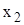 з Х їхні образи
з Х їхні образи  і
і  також різні, то відображення називається ін'єкцією (мал. 1.10, в). Відображення, що є одночасно сюр’єктивным і ин’єктивным (мал. 1.10, г), називається бієкцією (накладенням). У цьому випадку говорять, що
також різні, то відображення називається ін'єкцією (мал. 1.10, в). Відображення, що є одночасно сюр’єктивным і ин’єктивным (мал. 1.10, г), називається бієкцією (накладенням). У цьому випадку говорять, що 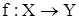 є взаємо-однозначне відображення, а між елементами Х і Y є взаємо-однозначна відповідність. При цьому зворотне відношення
є взаємо-однозначне відображення, а між елементами Х і Y є взаємо-однозначна відповідність. При цьому зворотне відношення 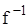 також взаємо-однозначне відображення,
також взаємо-однозначне відображення, 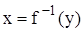 еквивалентно
еквивалентно 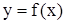 і
і  збігається з f.
збігається з f.
|
Будь-яке відображення f із Х в Y є елемент множини P  ,
,
що позначається також через 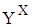 . Нагадаємо, що P
. Нагадаємо, що P  — це множина усіх підмножин прямого добутку
— це множина усіх підмножин прямого добутку  , а елементами останнього є упорядковані пари (х, у), де
, а елементами останнього є упорядковані пари (х, у), де 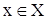 і
і 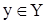 . Якщо f - взаємо-однозначне відображення, а множині Х и Y збігаються (X = Y), то
. Якщо f - взаємо-однозначне відображення, а множині Х и Y збігаються (X = Y), то 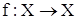 називають відображенням множині Х на себе. Елементи
називають відображенням множині Х на себе. Елементи  утворять тотожне відображення е, причому
утворять тотожне відображення е, причому 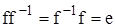 .
.






 Мал.1-10. Типи відображень.
а- відображення X у Y; б- відображення X на Y (сюр’єкція);
в- взаємно-однозначне відображення X у Y (ін’єкція);
г- взаємно-однозначне відображення X на Y (бієкція)
Мал.1-10. Типи відображень.
а- відображення X у Y; б- відображення X на Y (сюр’єкція);
в- взаємно-однозначне відображення X у Y (ін’єкція);
г- взаємно-однозначне відображення X на Y (бієкція)