Деякі елементи множини можна розглядати як еквівалентні в тому випадку, коли будь-який із цих елементів при деякому розгляді може бути замінений іншим. В цьому випадку говорять, що дані елементи знаходяться у відношенні еквівалентності.
Прикладами відношень еквівалентності є:
- відношення «бути на однім курсі» на множини студентів факультету;
- відношення «мати однаковий залишок при діленні на 3» на множини натуральних чисел;
- відношення паралельності на множини прямих площини;
- відношення подоби на множини трикутників і т.п.
Для того щоб дати чітке формулювання відношенню еквівалентності, будемо вважати, що термін «відношення еквівалентності» застосовується тільки у випадку, якщо виконуються наступні три умови:
1) кожний елемент еквівалентний самому собі;
2) висловлення, що два елементи є еквівалентними, не вимагає уточнення, який з елементів розглядається першим і який другим;
3) два елементи, еквівалентні третьому, еквівалентні між собою.
Приймемо для позначення еквівалентності символ 
. Тоді загальне визначення еквівалентності одержимо, записавши три вищенаведених умови у вигляді наступних співвідношень:
1) 
(рефлексивність);
2) 
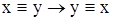(симетричність);
3) 
і 
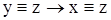(транзитивність).
Відношення А називається відношенням еквівалентності, якщо воно рефлексивне, симетричне і транзитивне.
Відношення еквівалентності знаходиться в тісному зв'язку з розбивкою множини. Нехай X- множина, на якій визначене відношення еквівалентності. Наприклад, Х - множина студентів курсу, а відношенням еквівалентності є відношення «бути в одній групі». Підмножину елементів, еквівалентних деякому елементу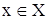 
, будемо називати класом еквівалентності. Так, група, у якій навчається студент Іванов, буде класом еквівалентності, еквівалентним студенту Іванову.
Нехай J — деяка множину індексів. Позначимо через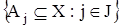 
множину класів еквівалентності для множини X. Очевидно, що всі елементи одного класу еквівалентності еквівалентні між собою (властивість транзитивності) і всякий елемент 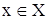може знаходитися в одному і тільки в одному класі. Але в такому випадку Х є об'єднанням множин Аj, що не перетинаються, так що повна система 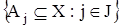класів є розбивкою множини Х. Таким чином, кожному відношенню еквівалентності на множини Х відповідає деяка розбивка множини Х на класи Аj.
Відношення еквівалентності на множині Х і розбивка цієї множини на класи називаються сполученими, якщо для будь-яких х та у з Х відношення виконується тоді і тільки тоді, коли х і у належать до того самого класу А цієї розбивки. Більш чіткому з'ясуванню зв'язку відношення еквівалентності з розбивкою множини допоможе порівняння прикладів даного розділу з прикладами з теми про операції над множинами.
У якості загального символу відношення еквівалентності використовується символ (іноді ~). Однак для окремих часткових відношень еквівалентності використовуються інші символи: = — для позначення рівності, çç - для позначення паралельності, Û — для позначення логічної еквівалентності.
