 =
= 
На мал. 1-7 приведені діаграми Эйлера-Венна для алгебраїчних виражень  і
і  . Обидва ці вирази дають ту саму множину, так що має місце тотожність
. Обидва ці вирази дають ту саму множину, так що має місце тотожність
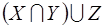 =
= 
3. Легко переконатися, що якщо YÍХ, то

Дійсно, всі елементи множини Y є в той же час і елементами множині X. Значить перетинання цих множин, тобто загальна частина множин Х и Y збігається з Y. В об'єднання множин Х і Y множину Y не внесе жодного елемента, що уже не входив би в нього, будучи елементом множини X. Отже,  збігається з Х.
збігається з Х.
4. Вважаючи Y=X і з огляду на, що ХÍХ, знаходимо

Доказ тотожностей алгебри множин за допомогою діаграми Ейлера-Венна в ряді випадків виявляється незручним. Є більш загальний спосіб установлення тотожності двох алгебраїчних виражень.
Нехай, як і колись, через  і
і  позначені два алгебраїчних вирази, що утворилися шляхом застосування операції об'єднання, перехрещення і доповнення до множин X, Y і Z. Для того щоб довести, що
позначені два алгебраїчних вирази, що утворилися шляхом застосування операції об'єднання, перехрещення і доповнення до множин X, Y і Z. Для того щоб довести, що  досить показати, що
досить показати, що  і що
і що  . В свою чергу, щоб показати, що
. В свою чергу, щоб показати, що  , потрібно переконатися, що з
, потрібно переконатися, що з  випливає
випливає  . Аналогічно, щоб показати, що
. Аналогічно, щоб показати, що  , потрібно переконатися, що з
, потрібно переконатися, що з  випливає
випливає  . Скористаємося цим методом, щоб довести ще декілька тотожностей.
. Скористаємося цим методом, щоб довести ще декілька тотожностей.
5. Доведемо тотожність 
Припустимо, що  , тобто що
, тобто що  Це значить, що
Це значить, що  і
і 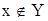 , тобто
, тобто  і
і  . Отже,
. Отже,  . Припустимо тепер, що
. Припустимо тепер, що  , тобто
, тобто 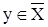 , і
, і 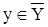 . Це значить, що
. Це значить, що 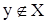 і
і  , тобто що
, тобто що 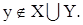 Отже,
Отже,  .
.
6. Тотожність

доведемо, привівши обидві його частини до однакового виду. Виконуючи операцію доповнення над обома частинами, одержимо  Ліва частина цього вираження дає Х Ç У. Те ж саме одержимо, перетворюючи праву частину за правилом
Ліва частина цього вираження дає Х Ç У. Те ж саме одержимо, перетворюючи праву частину за правилом  В літературі тотожності звичайно називаються тотожностями де-Моргана.
В літературі тотожності звичайно називаються тотожностями де-Моргана.
1.1.12. УПОРЯДКОВАНА МНОЖИНА
Поряд із поняттям множини як сукупності елементів важливим поняттям є поняття упорядкованої множині або кортежу. Кортежем називається послідовність елементів, тобто сукупність елементів, у котрої кожний елемент займає визначене місце. Самі елементи при цьому називаються компонентами кортежу (перша компонента, друга компонента і т.д.). Приклади кортежів: множина людей, що стоять у черзі; множина слів у фразі; числа, що виражають довготу і широту точки на місцевості, і т.п. В усіх цих множинах місце кожного елемента є цілком визначеним і не може бути довільно змінено.
Число елементів кортежу називається його довжиною. Для позначення кортежу використовуємо круглі дужки. Так, множина

є кортежем довжини n з елементами  . Кортежі довжини 2 називаються парами або упорядкованими парами, кортежі довжини 3 - трійками, 4 - четвірками і т.д. У загальному випадку кортежі довжини n називаються n-ками. Окремим випадком кортежу є кортеж (а) довжини 1 і порожній кортеж довжини 0, що позначається () або L.
. Кортежі довжини 2 називаються парами або упорядкованими парами, кортежі довжини 3 - трійками, 4 - четвірками і т.д. У загальному випадку кортежі довжини n називаються n-ками. Окремим випадком кортежу є кортеж (а) довжини 1 і порожній кортеж довжини 0, що позначається () або L.

Мал. 1-8. Проекції двох та триелементного кортежу.
На відміну від звичайної множині в кортежі можуть бути й однакові елементи: два однакових слова у фразі, однакові чисельні значення довготи і широти точки на місцевості і т.п.
Надалі будемо розглядати упорядковані множині, елементами яких є дійсні числа. Такі упорядковані множині називають точками простору або векторами. Так, кортеж  може розглядатися як точка на площині або вектор, проведений із початку координат у дану крапку (мал. 1-8 а)). Компоненти
може розглядатися як точка на площині або вектор, проведений із початку координат у дану крапку (мал. 1-8 а)). Компоненти  будуть проекціями вектора на осі 1 і 2
будуть проекціями вектора на осі 1 і 2
 .
.
Кортеж  може розглядатися як точка в тривимірному просторі, або як тривимірний вектор, проведений із початку координат у цю точку (мал. 1-8 б)). Проекції вектора на осі координат
може розглядатися як точка в тривимірному просторі, або як тривимірний вектор, проведений із початку координат у цю точку (мал. 1-8 б)). Проекції вектора на осі координат

Однак у даному випадку можна говорити про проекцію кортежу відразу на дві, осі, наприклад 1 і 2, тобто на координатну площину. Неважко бачити, що ця проекція являє собою двуелементний кортеж

Узагальнюючи ці поняття, будемо розглядати упорядковане n-елементну множину чисел  , як точку в уявлюваному n-мірному просторі, що називається іноді гіперпростором, або як n-мірний вектор. При цьому компоненти n-елементного кортежу а будемо розглядати як проекції цього кортежу на відповідні осі
, як точку в уявлюваному n-мірному просторі, що називається іноді гіперпростором, або як n-мірний вектор. При цьому компоненти n-елементного кортежу а будемо розглядати як проекції цього кортежу на відповідні осі

Якщо i, j,...,l номера осей, причому 1£ i < j <…<l £ n,то проекція кортежу а на осі i, j,...,l дорівнює:
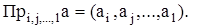
Проекцією кортежу на порожню множину осей є порожній кортеж
ПрÆ a =L






