Розбивка множини

Однією з операцій над множинами, що зустрічаються найчастіше, є операція розбивки множини на систему підмножин. Так, система курсів даного факультету є розбивкою множини студентів факультету, система груп даного курсу є розбивкою множини студентів курсу. Якщо N- безліч натуральних чисел, а А₀ і A₁-безлічі парних і непарних чисел, тоді система {А₀, A₁} буде розбивкою множини N. Множина натуральних чисел може бути розбита інакше, на множини чисел, що діляться на 3 без залишку, із залишком 1 і з залишком 2. Продукція підприємства розбивається на систему множин, що складаються із продукції першого сорту, другого сорту і браку. Подібні приклади можна було б продовжувати нескінченно.

Для того щоб дати поняттю розбивки суворе визначення, розглянемо деяку множину М і систему множин Œ ={X1,…,Xn}. Система множин Œ називається розбивкою множині М, якщо вона задовольняє наступним умовам:

1) будь-яка множина Х із Œ є підмножиною множині М

Œ

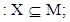
2) будь-які дві множини Х і Y із Œ не перетинаються

Œ, Œ Æ;

3) об'єднання всіх множин, що входять у розбивку, дає множину М

=M

До поняття розбивки ми повернемося при розгляді відношення еквівалентності, із яким воно дуже тісно пов'язане.