Перехрещенням множин Х і Y називається множина, що складається з усіх тих і тільки тих елементів, що належать як множині X, так і множині Y.
Перехрещення множин Х і Y позначається через 
. Формальне визначення
і 
Перехрещення множин іноді називають добутком множин і позначають XY. Однак властивості перехрещення множин трохи відрізняються від властивостей добутку в звичайному арифметичному розумінні. Тому цим терміном ми користуватися не будемо.
Приклад 1-4. Для множин Х і Y у прикладі 1-1 ХÇУ={2,4}.
Приклад 1-5. Для множин Х і Y у прикладі 1-2 ХÇY-множина відмінників групи, що проживають у гуртожитку.
Приклад 1-6. Розглянемо два кола, приведених на мал. 1-2. Якщо Х—множина точок лівого кола, а У — множина точок правого кола, то ХÇY являє собою заштриховану область, що є загальною частиною обох кіл.
| Мал. 1-2. Перехрещення множин | Мал. 1-3. Множини, що не перехрещуються |
Операція перехрещення дозволяє установити ряд співвідношень між двома множинами.
Множини Х і Y не перехрещуються, якщо вони не мають спільних елементів, тобто якщо Х Ç Y =Æ.
Приклад 1-7. множинами, що не перехрещуються, є
1) множини {1, 2, 3} і {4, 5, 6};
2) множина відмінників і множина невстигаючих студентів у групі;
3) множині точок кіл Х і У на мал. 1-3.
Говорять, що множині Х і Y знаходяться в загальному положенні, якщо виконуються три умови:
· існує елемент множини X, що не належить Y;
· існує елемент множини Y, що не належить X;
· існує елемент, що належить як X, так і Y.
Зазначимо одну відзнаку алгебри множин від алгебри чисел. Якщо a і b - два числа, то між ними може бути три співвідношення або три можливості:
a<b, a=b, b<a
Для двох множин Х і Y, однак, може не виконуватися жодне зі співвідношень:
Так, якщо Х - множина відмінників, а Y - множина студентів, що проживають у гуртожитку, то три раніше приведені співвідношення будуть означати:
XÌY- кожен відмінник обов'язково проживає в гуртожитку;
X=Y- в гуртожитку проживають усі відмінники і тільки вони;
YÌX- всі студенти, що проживають у гуртожитку, є відмінниками.
Очевидно, що ці співвідношення не вичерпують усіх можливостей. Насправді, як випливає з попередніх визначень, між двома множинами Х і Y може бути одне з п'ятьох відношень:
Х і Y знаходяться в загальному положенні.
Поняття перехрещення можна поширити і на більше чим два числа множин. Розглянемо систему множин Œ ={Х1,...,Хn}. Перехрещення цих множин записується у вигляді
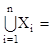
і уявляє собою множину, елементи які належать кожному з множин системи Œ.
Неважко бачити, що перехрещення множин має комутативну властивість
і асоціативну 
Зауважимо також, що має місце співвідношення
ХÇÆ=Æ
аналогічне співвідношенню а´0=0 у звичайній алгебрі. Т.ч. порожня множина відіграє роль нуля в алгебрі множин. Співвідношення 
та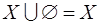 
показує, що пуста множина відіграє роль 0 в алгебрі множин.
