Над множинами можливо здійснювати дії, які багато чим нагадують складення або множення в елементарній алгебрі.
Нехай a та b – деякі числа, a + b їх сума, а a*b – їх добуток. Сума та добуток чисел мають наступні властивості, що називаються законами алгебри:
1. 
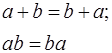- комутативний закон, або закон переміщення;
2. 
- асоціативний або сполучувальний закон;
3. 
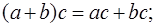- дистрибутивний або розподільчий закон.
Зауважимо, що в асоціативному та комутативному законах можна замінити складення перемноженням а перемноження складанням. Але в дистрибутивному законі подібної симетрії немає. Якщо в цьому законі замінити складення множенням, а множення то прийдемо до абсурду: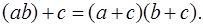 
Питається. Чи завжди це так? Чи не існує алгебри, в якій дистрибутивний закон був би також симетричним відносно складення і множення, як комутативний та асоціативний закони?
Виявляється, що існує алгебра, а точніше алгебра множин, в якій всі три закони симетричні відносно дій складення і множення.
Збіжність між діями складання і множення проявляється також в існуванні двох чудових чисел 0 та 1, що додавання першого та множення на друге не змінюють жодного числа:
Зауважимо, що друге співвідношення отримується із першого заміною (+) на (*) та 0+1.
Але і тут збіжність між діями складання та множення не полягає особливо далеко. Так, число 0 грає декілька особливу роль по відношенню з усіма іншими числами в тому числі і одиницею. Ця особлива роль числа 0 витікає із співвідношення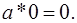 
Якщо ми в цьому виразі замінимо (*) на (+) та 0 на 1, то приходимо до співвідношення , яке не буде вірним. Як ми побачимо далі, збіжність між нулем і одиницею в алгебрі множин буде значно більшою, ніж в звичайній алгебрі.
1.1.5. ОБ’ЄДНАННЯ МНОЖИН.
Об’єднанням множин Х та Y називається множина , яка складається із всіх тих і тільки тих елементів, що належать хоч би одній із множин Х,Y, тобто належить Х або Y. Об’єднання множин Х та Y визначається через .
Формальне визначення: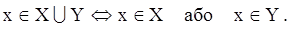 
Об’єднання множин іноді називають сумою множин і позначають Х+Y. Але властивості об’єднання множин де в чому відрізняються від властивостей суми в звичайному арифметичному розумінні. Тому цим терміном ми користуватись не будемо.
Приклад 1-1.
Якщо 
і 
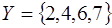то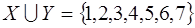 
.
Приклад 1-2.
Якщо Х – множина відмінників в групі, а Y- множина студентів, що живуть в гуртожитку, то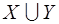 
- множина студентів, які або вчаться на відмінно, або проживають в гуртожитку.
Приклад 1-3.
Розглянемо два круги, що приведені на малюнку 1. Якщо Х – множина точок лівого кругу, а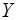 
- множина точок правого кругу, то 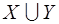уявляє собою заштриховану область, обмежену обома кругами.
 |
Поняття об'єднання можна поширити і на більше число множин. Через Œ 
позначимо сукупність n множин X1,...,Xn, називану іноді системою множин. Об'єднання цих множин 
, 
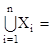являє собою множину, що складається з усіх тих і тільки тих елементів, що належать хоча б одному з множин системи Œ.
Для об'єднання множин справедливі комутативні й асоціативний закони
справедливість яких випливає з того, що ліва і права частини рівностей утворюються із одних і тих же елементів. Далі
ХÈÆ=Х
Це також очевидне співвідношення, тому що порожня множина не містить елементів, а значить Х і ХÈÆ складаються із тих самих елементів. З того, що ХÈÆ=Х видно, що порожня множину Æ відіграє роль нуля в алгебрі множин. Тут має місце аналогія з виразом а+0 = а в звичайній алгебрі.