МНОЖИНИ.
АЛГЕБРА МНОЖИН.
ВИЗНАЧЕННЯ МНОЖИНИ.
Множиною називається сукупність визначених об’єктів, які можливо розрізнити і розглядати як єдине ціле.
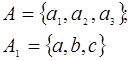
визначення визначення
конкретної елемента
множини множини
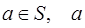належить множині S.
не належить множині S.
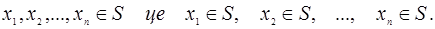
Множини бувають: скінченні (якщо кількість елементів скінчена) і нескінчені (якщо кількість елементів нескінченно).
Множини можуть задаватися різними способами. Наприклад:
1) якщо Х- множина відмінників групи, то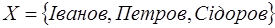 
- це спосіб завдання множини перерахуванням скінченої множини;
2) 
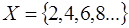- це спосіб завдання перерахуванням нескінченої множини;
3) описовий спосіб завдання множин:
- 
. 
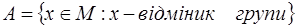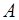складається із елементів 
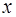множини 
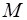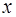, являється відмінником групи. Якщо не визиває сумнівів із якої множини беруться елементи 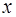, то 
;
- 
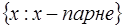- множина парних чисел;
- 
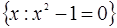- множина 
.
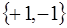Нехай С- множина цілих чисел. Тоді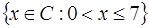 
є множина 
.
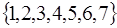Пустою множиною називають множину, яка не включає жодного елемента. Пусту множину визначають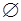 
. Наприклад: 
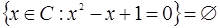. Пусту множину будемо умовно відносити до скінченої множини.
Дві множини називаються рівними, якщо вони складаються із одних і тих же елементів, тобто уявляють собою одну і ту ж множину.
Множини X та Y не рівні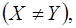 
якщо або в множині Х є елементи, що не належать Y, або в множині Y є елементи, що не належать Х.
Для будь яких множин Х,Y та Z:
- 
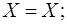
- якщо 
, то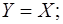 
- якщо , та 
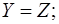то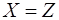 
.
Із визначення рівності множин витікає, що порядок елементів в множинах несуттєвий. Так, наприклад, множини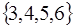 
та множини 
уявляють собою одну і ту ж множину.
Домовимося, що в множинах не буває однакових елементів. Запис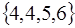 
треба розглядати як некоректну і замінити її на 
.
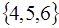