Множина Х являється підмножиною Y, якщо будь-який елемент множини Х належить і множині Y.
Нехай Y множина студентів групи, а Х – множина відмінників цієї ж групи. Так як кожний відмінник групи являється в той же час і студентом цієї групи, то множина Х являється підмножиною множини Y.
Багато визначень теорії множин зручно давати в вигляді математичних виразів, що містять деякі логічні символи. Для визначення підмножин використаємо два таких символи:
- символ, що називається квантором та значить “будь – який”, “який би не був”, “для всіх;
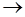- символ слідства (імплікації).
або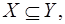 
що означає “Y містить Х”.
Символ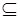 
означає вміщення. Якщо необхідно підкреслити, що Y містить і інші елементи, крім елементів із Х, то використовують символ строгого включення 
: 
Зв’язок між символами та 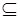дається виразом
та 
;
(рефлексивність);
(транзитивність);
.
