Пусть БДР задачи (2.4.1) соответствует переменным 
. Тогда ограничения задачи (2.4.1) могут быть преобразованы к виду
(2.5.1)
...................................
Тогда векторы u и v предыдущего параграфа можно выразить через x следующим образом:
, 
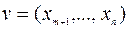
Согласно (2.4.7), вектор критерия оптимальности 
может быть получен посредством преобразования первоначальной целевой функции, записанной в виде уравнения
.
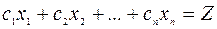Из этого уравнения вычитаются уравнения ограничений, умноженные соответственно на 
. В результате будет получено новое уравнение
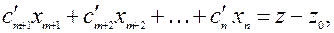(2.5.2)
где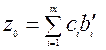 
. Эта процедура соответствует исключению переменных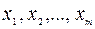 
из целевой функции посредством равенств ограничений. Коэффициенты левой части полученного уравнения - это компоненты вектора критерия оптимальности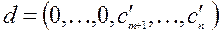 
Пример. Решить задачу (1а).
Набор 
, 
, 
является БДР. Функция 
, имеющая нулевое значение, выражена через небазисные переменные. Коэффициенты при 
и 
отрицательные. Так как коэффициент при больше по модулю, выберем переменную для изменения. Существует предел изменения переменной поскольку ограничения (2.4.1) должны выполняться, и переменные 
, 
оставаться неотрицательными.
Поскольку 
,
то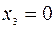 
при 
.
Поскольку 
,
то 
при 
.
Поэтому 
.
Этот итерационный процесс удобно представить в симплекс- таблицах
| итерация | базис | значение | 
| 
|
|
| операции над строками |
| - z | -2 | -4 | 
| ||||
| 
| ||||||
| 5 * | 
|
| - z | -2/5 | 4/5 | 
| ||||
|
| 7/5 * | -4/5 | 
| ||||
|
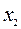
| 2/5 | -1/5 | 
|
| - z | 2/7 | 4/7 | |||||
|
| 5/7 | -4/7 | |||||
|
| -2/7 | 3/7 |
Справа от таблиц приведены операции со строками. Штрихом обозначается вновь полученная строка, которая помещается в следующую таблицу. Строка, соответствующая 
-функции, нумеруется как нулевая строка. Звездочкой обозначается элемент, соответствующий столбцу, вводимому в базис с наибольшим по модулю отрицательным значением нулевой строки, и строке, соответствующей той базисной переменной, которая убывает до нуля и выводится из базиса.
Рассмотрим симплекс-метод в таблицах. Предположим, что на некоторой произвольной итерации задача ЛП представлена в форме (2.5.2), (2.5.1), а коэффициенты внесены в таблицу:
| базис | значение | 
|
| ... | 
| ... | 
| 
| ... | 
| ... | 
|
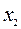
| - z | 
| 
| 
| 
| ||||||||
| 
| 
| 
| 
| ||||||||
| 
| 
| 
| 
| ||||||||
| 
| 
| 
| 
| ||||||||
| 
| 
| 
| 
|
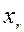
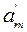
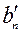
Итерация процесса состоит из трех шагов.
1) Найти переменную для включения в базис. Переменные 
небазисные. Находим наименьший из коэффициентов 
. Пусть это коэффициент 
. Если 
, то увеличение 
приведет к убыванию функции 
. Будем выбирать столбец с наименьшими значениями 
. Если все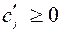 
, то значение функции не может быть уменьшено, решение найдено.
2) Найти переменную для исключения из базиса. Следует найти для каждой базисной переменной величину, на которую можно увеличить не нарушая условия неотрицательности 
Чтобы не нарушалось условие неотрицательности ни для одной базисной переменной следует выбрать
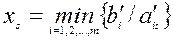
Если этот минимум достигается в строке 
, то 
обращается в 0. Другие базисные переменные останутся неотрицательными. Элемент 
называется ведущим элементом, строка - ведущей строкой, столбец 
- ведущим столбцом.
3) Построить новую форму задачи типа (2.5.2), (2.5.1) для базисных переменных. Следует коэффициент при в ведущей строке сделать равным 1, поделив строку на 
Затем исключить коэффициенты при из других строк, прибавляя или вычитая ведущую строку.
